Biot-Savart Law Formula

The Biot-Savart Law relates the currents as sources of the magnetic fields. The magnetic field results from a current distribution that involves the vector product. Its units are given in Tesla (T). The expression for the modulus of the differential magnetic field is:

Magnetic field = Integration over the cable path of (vacuum permeability constant/4 π * current * (sine of the angle between current direction and cable position vector)/ (cable position)²) * line element

The equation is:

B = ∫ (μ0 / 4 π) I dl sin(θ)/r²

Where:

μ0: vacuum permeability

B: magnetic field

I: current intensity flowing in the cable

θ: angle between the current path and the position of the cable

r: distance from the origin of coordinates to the cable

dl: line element

Biot-Savart Formula Question:

1) Find the magnitude and direction of the magnetic field at the center of a loop carrying a current I=2 A with radius R=20 cm.

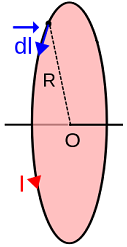
Answer:

Note that dl is perpendicular to r, so the angle is 90°, dB will point out along the axis of the ring.

The value of μ0 = 4 π *10^(-7) T *m/A, from the formula of Biot-Savart

B = ∫ (4π *10^(-7) T*m/A / 4π ) 2 A dl Sin(90°) /R²

B= 10^(-7) T*m/A * 2 A /(0.2 m)² ∫ dl

Since ∫ dl = 2 π R,

B = 10^(-7) T*m/A * 2 A *2 π 0.2 m/(0.2 m)²

B = 10^(-7) T*m/A * 2 A *2 π /(0.2 m) = 62.83*10^(-7) T