Center of Mass Formula
The center of mass is a point of balance of an object or a group of objects. The center of mass can be found for any one, two-, or three-dimensional object, and so the units are meters (m) in each dimension. The formula given here is for the center of mass in one dimension.
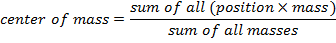
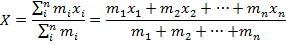
X = center of mass (m)
mi = mass of a part of an object (kg)
xi = position of the part of an object (m)
Center of Mass Formula Questions:
1) The minute hand of a clock consists of an arrow and a circle connected by a thin piece of metal with negligible mass. The arrow has a mass of 15.0 g, and the circle has a mass of 60.0 g. If the circle is at position 0.000 m, and the arrow is at position 0.100 m, where is the center of mass?
Answer: The center of mass of the minute hand can be found using the formula:
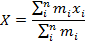
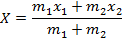
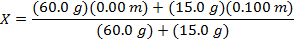
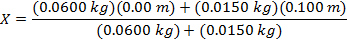
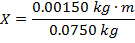
X = 0.020 m
The center of mass is 0.020 m from the circle.
2) A hanging light fixture has the following lights attached to it: i) a 0.10 kg light at position 0.00 m, ii) a 0.20 kg light at position 0.20 m, iii) a 0.80 kg light at position 0.80 m, and iv) a 0.10 kg light at position 1.0 m. Where is the center of mass?
Answer: The center of mass of the minute hand can be found using the formula:
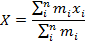
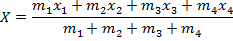
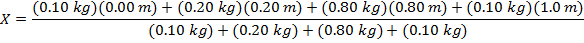
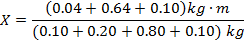
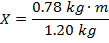
X = 0.65 m
The center of mass is at position 0.65 m.
|
Related Links: |
