Conservation of Energy Formula

An object, or a closed system of objects, can have both kinetic and potential energy. The sum of the kinetic and potential energy of the object or system is called the total mechanical energy. If no outside forces act on the system, then the total mechanical energy is conserved. Energy can change from kinetic to potential energy, and back, without reducing the total energy. The sum of the kinetic and potential energy at an initial time will be equal to the sum of the kinetic and potential energy at any other time.

Often, a mechanical system is not fully closed. Either the system can do work on the surroundings (for example, by heating), or work can be done on the system (for example, air resistance, or friction). In this case, a term for "other work" is added to the formula to account for the change in total mechanical energy. The unit of energy and work is Joules (J).

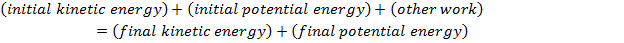
K₁ = initial kinetic energy (Joules, J)

U₁ = initial potential energy (J)

w_other = other work, gained or lost to the system (J)

K₂ = final kinetic energy (J)

U₂ = final potential energy (J)

Conservation of Energy Formula Questions:

1) An astronaut on the moon picks up a rock, and holds it out. At that moment, the rock is at rest, and has 5.00 J of gravitational potential energy. A moment later, the rock hits the surface of the moon. What was the kinetic energy of the rock immediately before it hit the surface?

Answer: The stored potential energy of the rock is in the form of gravitational potential energy. This means that the potential energy decreases as the rock falls toward the surface of the moon. At the moment before the rock reaches the surface, the rock's gravitational potential energy is zero. Since there is no air on the moon, there is no air resistance, and so the total mechanical energy is conserved. The rock is released from rest, and so its initial kinetic energy is zero. To summarize the known values:

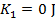
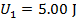
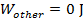
k₂ = unknown

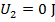
Using these values, and the formula for conservation of energy, the final kinetic energy can be found:

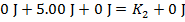
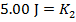
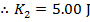
The kinetic energy of the moon rock immediately before it hits the surface of the moon is 5.00 J.

2) A block of wood on a table is forced against a horizontal spring. This compresses the spring, so that it has 18.00 J of elastic potential energy. The block is then released, with causes the spring to move the block across the table. A moment later, the spring has 1.50 J of elastic potential energy remaining, and the block is moving with 14.00 J of kinetic energy. How much of the total mechanical energy of the block-spring system was lost to friction between the block and the table?

Answer: The spring initially stored 18.00 J of elastic potential energy. At that moment, the block was at rest, and so its kinetic energy was zero. The remaining potential energy and kinetic energy of the block at a later time are also given. To summarize the known values:

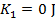
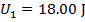
w_other = unknown

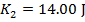
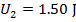
Using these values, and the formula for conservation of energy, it is possible to determine how much work was done by the system, in the form of friction:

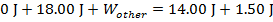
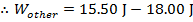
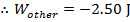
The other work is -2.50 J. This means that mechanical energy was lost to the system. In this case, the energy was lost in the form of friction between the block and the table.