Cross product Formula
The vector product or cross product is a binary operation between two vectors in a three-dimensional space. The result is a vector perpendicular to the vectors that multiply, and therefore normal to the plane that contains them. Due to its ability to obtain a vector perpendicular to two other vectors, whose direction varies according to the angle formed between these two vectors, this operation is often applied to solve mathematical, physical or engineering problems.
vector a X vector b = module of the vector a * module of the vector b * sine of the angle between vectors a and b * normal of the plane formed by vectors a and b.
The equation is:
,
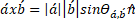we have,
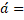vector a.
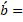vector b.
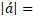module of the vector a.
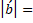module of the vector b.
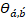= angle between vectors a and b.
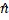= * the normal of the plane formed by vectors a and b.
Another way to calculate the vector product in Cartesian space R3 isthrough the determinant of the following matrix.
| I j k |
| ax ay az |
| bx by bz |
And the determinant is:
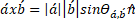= (ay*bz - az*by)i + (az*bx - ax*bz)j + (ax*by - ay*bx)k
Cross product Questions:
1) Given the vector a = 1i-3j and the vector b = -3i+2 and the angle between them is 134.69°, calculate the vector product between a and b.
Answer: The first thing to do is to calculate the module of both vectors.
|a|=((1)2+(-3)2)-1/2 = 3.16
|b|=((-3)2+(2)2) = 3.6
then, the normal of the plane formed by vectors a and b is k because they are in the xy plane. Then we calculate the cross product between a and b:
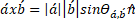= 3.16* 3.6 * sin(134.69°)k = 8.09 k.
a x b = 8.09 k.
2) Given the vector a = 4i+3j-2k and the vector b = i-2j-4k, calculate the vector product between a and b.
Answer: as we do not know the angle formed by vectors a and b we will use the formula of the determinant:
ax = 4.
ay = 3.
az = -2.
bx = 1.
by = -2.
bz = -4.
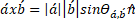= (ay*bz - az*by)i + (az*bx - ax*bz)j + (ax*by - ay*bx)k=(3*(-4)- (-2)*(-2))i + ((-2)*1 - 4* (-4))j + (4*(-2)- 3*1)k = -16i + 14j-11k.
axb = -16i +14j - 11k.
|
Related Links: |