Doppler Effect Formula
The sound that a listener hears can change if the source of the sound and the listener are moving relative to each other. This is called the Doppler Effect. When the listener and the source are moving closer, the frequency heard by the listener will be higher than the frequency of the sound emitted by the source. When the listener and the source are moving away from each other, the frequency heard by the listener will be lower than the frequency of the sound from the source. The unit of sound frequency is usually written as Hertz (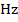 ), where one Hertz is a cycle per second (
), where one Hertz is a cycle per second (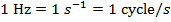 ).
).
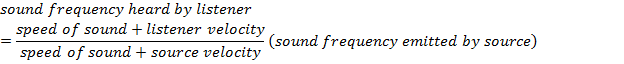
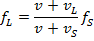
fL = frequency of sound heard by the listener (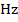 , or
, or 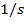 )
)
v = speed of sound in the medium (m/s)
vL = listener's velocity (m/s)
vs = velocity of the sound source (m/s)
fs = frequency of sound emitted by the source (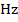 , or
, or 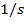 )
)
Doppler Effect Formula Questions:
1) A person standing on the sidewalk listens as a police car approaches. The police car's siren is on, and the sound it produces has a single frequency of 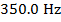 . The police car's speed is 28.0 m/s, and the speed of sound in air is 340.0 m/s. This question has two parts: a) what is the frequency of the sound heard by the person on the sidewalk as the police car approaches? b) Once the police car drives by, what is the sound of the siren heard by the person on the sidewalk as the police car gets farther away?
. The police car's speed is 28.0 m/s, and the speed of sound in air is 340.0 m/s. This question has two parts: a) what is the frequency of the sound heard by the person on the sidewalk as the police car approaches? b) Once the police car drives by, what is the sound of the siren heard by the person on the sidewalk as the police car gets farther away?
Answer:
a) The first step is to establish a coordinate system. The positive direction is defined to be from the listener to the source. The car is the source, and in part a) of this question, the police car is approaching the listener, and so the car's velocity is negative. The known values are therefore:
v = 340.0 m/s
vL = 0 m/s
vs = -28.0 m/s
fs = 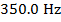
Using these values and the Doppler frequency formula, the frequency of the sound heard by the listener as the car approaches is:
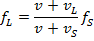
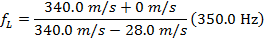
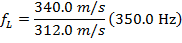
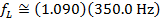
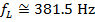
As the police car approaches the listener standing on the sidewalk, the frequency of the sound heard by the listener is 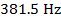 .
.
b) As in the first part, the first step is to establish a coordinate system. The positive direction is defined to be from the listener to the source, which is now moving away from the listener. In this case, the car's velocity is positive. The known values are therefore:
v = 340.0 m/s
vL = 0 m/s
vs = 28.0 m/s
fs = 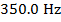
Using these values and the Doppler frequency formula, the frequency of the sound heard by the listener as the car gets farther away is:
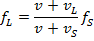
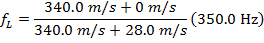
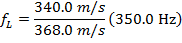
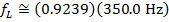
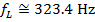
As the police car gets farther away from the listener standing on the sidewalk, the frequency of the sound heard by the listener is 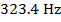 .
.
2) Imagine you are in a car traveling on a road next to train tracks. As a train approaches, it blows its horn, producing a sound with a single frequency of 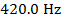 . The speed of your car is 18.0 m/s, the speed of the train is 32.0 m/s, and the speed of sound in air is 340.0 m/s. What is the frequency of the sound you would hear in the car?
. The speed of your car is 18.0 m/s, the speed of the train is 32.0 m/s, and the speed of sound in air is 340.0 m/s. What is the frequency of the sound you would hear in the car?
Answer: The first step is to establish a coordinate system. The positive direction is defined to be from the listener to the source. The train's horn is the source, and so the train's velocity is negative, and your velocity (in the car) is positive. The known values are therefore:
v = 340.0 m/s
vL = +18.0 m/s
vs = -32.0 m/s
fs = 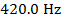
Using these values and the Doppler frequency formula, the frequency of the sound heard by you (the listener) as the train approaches is:
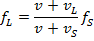
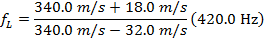
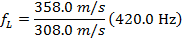
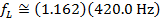
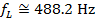
As you and the train approach each other, the frequency of the sound you hear from the train's horn is 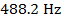 .
.
|
Related Links: |
