Force of attraction Formula
The law of attraction between bodies with mass was described by Sir Isaac Newton which states that objects are attracted to each other by the simple fact being massive. What causes this attraction is gravitational force, which is why Newton called this law the Universal Law of Gravitation. The interaction between two bodies of mass m1 and m2 is described in terms of an attractive force, whose direction is the straight line passing through the center of the two bodies and inversely proportional to the square of the distance separating the two bodies. This force explains, among many other things, why the planets orbit.
Force of attraction = Gravitational constant* mass 1 * mass 2 / (distance between bodies) ^2
The equation is written
F = G*m1*m2/d2
We have:
F = force of attraction
G = 6.67*10-11 Nm2/kg2 = gravitational constant
m1 = mass 1
m2 = mass 2
d = distance between bodies
Force of attraction Questions:
1) A mass of 800 kg and another of 500 kg are separated by 3m. What is the attraction force experienced by the mass?
Answer: To get the attraction force between these masses we use the above equation, where m1 = 800 kg, m2 = 500 kg, d = 3 m.
F = G*m1*m2/d2
F = (6.67*10-11 Nm2/kg2)(800 kg)(500 kg)/ (3 m)2
F = (6.67*10-11 Nm2/kg2)(400000 kg 2)/9 m2
F = (6.67*10-11 Nm2/kg2)(44,444.4 kg 2/m2)
F = 2.964*10-6 N.
2) At what distance are two masses of 60 kg and 70 kg, if the magnitude of the force with which they are attracted is 9*10-4 N?
Answer: To get the distance that separates the masses, we must clear d of the previous equation.
F = G*m1*m2/d2
d2= G*m1*m2/F
d = 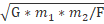
where m1 = 60 kg, m2 = 70 kg, F = 9*10-4 N,
d = 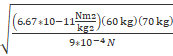
d = 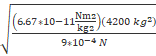
d = 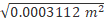
d = 0.018 m.
|
Related Links: |
