Inverse Square Law Formula

The inverse square law describes the intensity of light at different distances from a light source. Every light source is different, but the intensity changes in the same way. The intensity of light is inversely proportional to the square of the distance. This means that as the distance from a light source increases, the intensity of light is equal to a value multiplied by 1/d²,. The proportional symbol, 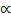, is used to show how these relate. The relationship between the intensity of light at different distances from the same light source can be found by dividing one from the other. The formula for this is shown below. Visible light is part of the electromagnetic spectrum, and the inverse square law is true for any other waves or rays on that spectrum, for example, radio waves, microwaves, infrared and ultraviolet light, x rays, and gamma rays. The intensity of visible light is measured in candela units, while the intensity of other waves is measured in Watts per meter squared (W/m²).

Proportional:

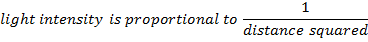
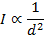
I = light intensity (candela, W/m²)

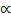means "is proportional to"

d = distance from a light source (m)

Intensity at different distances:

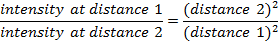
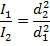
I₁ = light intensity at distance 1

I₂ = light intensity at distance 2

d₁ = distance 1 from light source (m)

d₂ = distance 2 from light source (m)

Inverse Square Law Formula Questions:

1) If a bright flashlight has a light intensity of 15.0 candela at a distance 1.00 m from the lens, what is the intensity of the flashlight 100.0 m from the lens?

Answer : The intensity at the farther distance can be found using the formula:

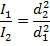
If d₁ = 1.00 m from the lens, and d₂ = 100.0 m from the lens, then I₁ = 15.0 candela, and we need to solve for I₂. This requires rearranging the equation:

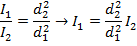
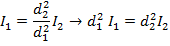
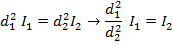
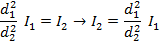
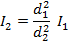
Now, substitute the values that are known in to the equation:

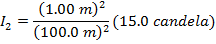
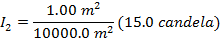
I₂ = (0.0001)(15.0 candela)

I₂ = 0.0015 candela

The intensity of the flashlight at a distance of 100.0 m is 0.0015 candela.

2) The intensity of a radio signal is 0.120 W/m² at a distance of 16.0 m from a small transmitter. What is the intensity of the signal 4.00 m from the transmitter?

Answer: The intensity at the near distance can be found using the formula:

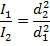
If d₁ = 4.00 m from the transmitter, and d₂ = 16.0 m from the transmitter, then

I₂ = 0.120 W/m², and we need to solve for I₁. This requires rearranging the equation:

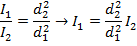
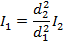
Now, substitute the values that are known in to the equation:

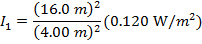
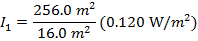
I₁ = (16.0)(0.120 W/m²)

I₁ = 1.92/m²

The intensity of the radio signal 4.00 m from the transmitter is 1.92 W/m².