Kirchhoff's Junction Rule Formula

In a closed circuit, there can be any number of circuit elements, such as batteries and resistors. The circuit can branch, creating "junctions", where the circuit separates or recombines. The sum of the currents in and out of a circuit junction must be zero. This is known as Kirchhoff's Junction Rule. Current is measured in Amperes (A).

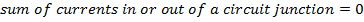
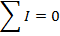
I = current, (Amperes, A)

Kirchhoff's Junction Rule Formula Questions:

1) The circuit in the figure below consists of two resistors and a voltage source (battery). The current before junction "a" is I_a, the current through resistor R₁ is I₁, and the current through resistor R₂ is I₂. Values are given in the figure for I_a and I₂. Based on this figure, what is the value of current I₁?

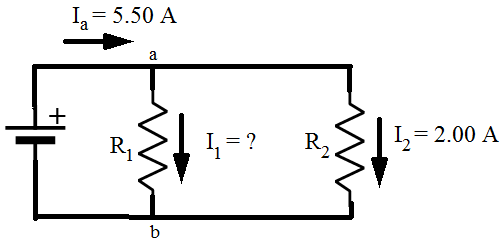
Answer: Kirchhoff's Junction Rule states that the sum of the currents in and out of a junction must be equal to zero. In this case, I₁ is connected to junction "a", and the sum of the currents in and out of junction "a" can be used to find the value of I₁. The direction of the currents at the junction are important. In this case, current is shown flowing through the circuit in a clockwise direction. This means that there is one current flowing in, and two currents flowing out of junction "a". The sum of the currents in and out of junction "a" is:

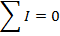
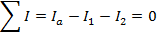
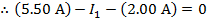
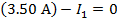
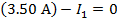
The value of I₁ can be found by rearranging the formula above:

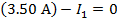
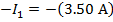
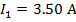
The value of current I₁ is 3.50 A(Amperes).

2) The circuit in the figure below consists of three resistors and a voltage source (battery). The current before junction "a" is I_a, the current before junction "b" is I_b, the current through resistor R₁ is I₁, the current through resistor R₂ is I₂ , and the current through resistor R₃ is I₃. Values are given in the figure for I_a, I₁, and I₂. Based on this figure, what is the value of current I₃?

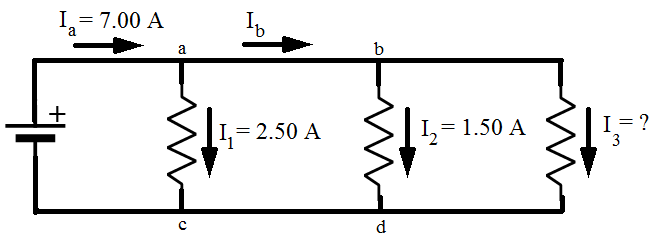
Answer: Kirchhoff's Junction Rule states that the sum of the currents in and out of a junction must be equal to zero. In this case, I₃ is connected to junction "b". The directions of the currents at the junctions are important. In this case, current is shown flowing through the circuit in a clockwise direction. The sums of the currents flowing in and out of junctions "a" and "b" can be used to find the value of I₃. The sum of the currents in and out of junction "a" is:

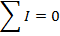
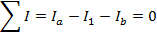
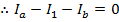
The sum of the currents in and out of junction "b" is:

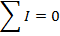
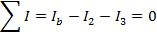
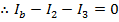
These two equations can be combined to solve for I₃. The common way to express this is that we have "two equations and two unknowns". The values of I_b and I₃ are unknown, but with two equations, there is enough information to solve the problem. The equations can be labeled (1) and (2):

(1)

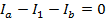
(2)

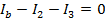
Equation (1) can be rearranged to isolate I_b on the left side of the equal sign:

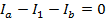
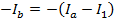
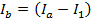
Now, this equation for I_b can replace I_b in equation (2):

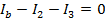
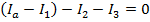
This can now be rearranged to solve for I₃:

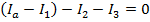
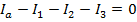
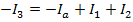
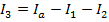
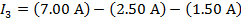
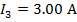
The value of current I₃ is 3.00 A(Amperes).