Length Contraction Formula

Special relativity states that the distance between two points can differ in different reference frames. The distance between points, and therefore the length, depends on the velocity of one reference frame relative to another. In one reference frame, an object being measured will be at rest. This is called the proper length, and is labeled Δl₀. In another reference frame, an observer will see the object moving. The length of the object in this reference frame is observed length, and is labeled Δl. The observed length is always shorter than the proper length. This effect is called length contraction. Both Δl₀ and Δl are measured in meters (m).

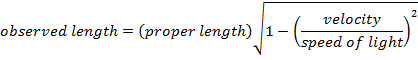
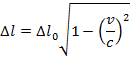
Δl = the observed length, in the reference frame in which the object is moving (m)

Δl₀ = the proper length, in the reference frame in which the object is at rest (m)

v = velocity (m/s)

c = speed of light (3.0 x 10⁸ m/s)

Length Contraction Formula Questions:

1) A crew member of a spaceship measures the ship's length to be 100 m. The ship flies past Earth at a speed of 0.900 times the speed of light. If observers on Earth measure the length of the ship, what would they measure?

Answer: The reference frame of the ship's crew member is the one in which the ship is at rest. The crew member's measured length is the proper length, Δl₀. The observers on Earth measure the observed length, Δl. The length of the ship in the reference frame of the Earth-based observers can be found using the formula:

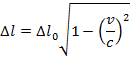
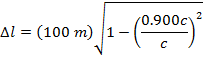
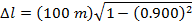
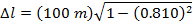
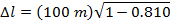
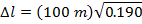
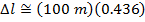
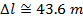
The observers on Earth measure the length of the ship to be 43.6 m. This is less than the 100 m length measured in the reference frame of the ship's crew member.

2) Cosmic rays colliding with Earth's upper atmosphere produce high-energy particles called muons. An observer detects that a muon has been created 55.0 km above the surface of the Earth. Another observer detects the muon when it arrives at the surface. The observers determine that the muon was moving at 2.97 x 10⁸ m/s. In the muon's reference frame, what was the distance between where it was created and the surface of the Earth?

Answer: The two positions to consider are the position at which the muon was created, and its arrival at the surface of the Earth. The distance between these positions in the reference frame of the observers is Δl. In the muon's reference frame, the distance between the points in the proper length, Δl₀. The distance in the reference frame of the observers is known, and so the distance in the muon's reference frame can be found by rearranging the length contraction formula:

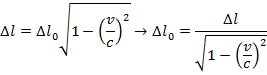
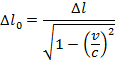
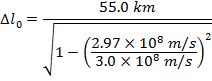
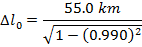
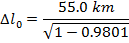
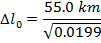
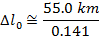
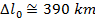
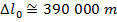
In the muon's reference frame, the distance between where it is created and the surface of the Earth is approximately 390 km, or 390 000 m. This is significantly longer than the contracted length, 55.0 km or 55 000 m, measured by the observers.