Potential Energy: Two-Body Gravitation Formula

Potential energy is energy that is stored in a system. There is the possibility, or potential, for it to be converted to kinetic energy. Any two objects with mass are attracted to each other by gravity. In space, it is possible to find the potential energy of gravity between two objects separated by a distance. This potential energy formula contains a constant, G, which is called the "universal gravitational constant". Its value is = 6.673 x 10^-11 (N∙m²)/kg² . The unit of potential energy is the Joule (J), where 1 J = 1 N∙m = 1 kg m²/s² .

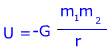
U = potential energy of gravity between two objects

G = the universal gravitational constant, G = 6.673 x 10^-11 (N∙m²)/kg²

m₁ = mass of one of the objects

m₂ = mass of the second object

r = the distance between the centers of mass of the two objects

Potential Energy: Two-Body Gravitation Formula Questions:

1) Two asteroids are drifting away from each other. One asteroid has a mass of 240000 kg, and the other has a mass of 100000 kg. What is the change in gravitational potential energy as their centers of mass move from 100 m apart to 1000 m apart? Give the final answer with four places after the decimal.

Answer: This question asks for a change in potential energy. We will use the symbol ∆ to mean "the change in". So, we will use the equation to find ∆U, the change in gravitational potential energy:

∆U = U_final - U_initial

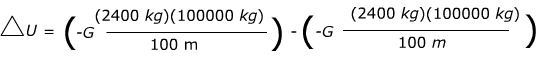
Take out common factors

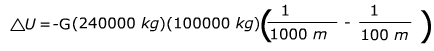
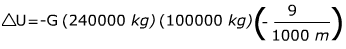
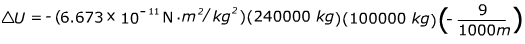
∆U = 0.0144 N∙m

∆U = 0.0144 J

The change in gravitational potential energy as the asteroids move away from each other is 0.0144 Joules.

2) An astronaut is outside performing a spacewalk near the International Space Station. With her spacesuit and all equipment, she has a mass of 200 kg. The space station has a mass of 419,600 kg. What is the gravitational potential energy when she is 10.0 m from the center of mass of the space station?

Answer: The formula can be used to find the potential energy:

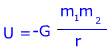
U = 0 when the distance between the astronaut and the space station is infinite, and so this equation represents the change in potential energy if you bring the astronaut from an infinite distance away to a position 10.0 m from the center of mass of the station. The force acting on the astronaut is away from the position where U = 0, and this is why the equation has a negative sign, and the potential energy we find will be negative.

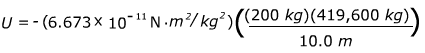
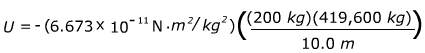
U = -0.000560 N∙m

U = -5.60 x 10^-4 J

The gravitational potential energy of her position 10.0 m from the center of mass of the station is -5.60 x 10^-4 J.