Reynold's Number Formula

The Reynold's number is used to describe fluid flow. Flow can be laminar, turbulent, or between these two states (a transient flow). It is found by dividing the fluid's inertial force by its viscous force. The Reynold's number is unitless. Low Reynold's numbers indicate laminar flow, meaning it is smooth and constant. High Reynold's numbers indicate turbulent flow, meaning it is chaotic. Values in between indicate transient flow, meaning the flow changes with time. The Reynold's number can be used for a number of fluid flow situations, as well as objects moving through fluids.

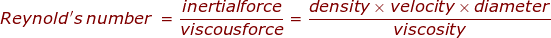
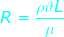
R = Reynold's number (unitless)

ρ = the density of the fluid (kg/m³)

v = the velocity of the fluid (m/s)

L = the "characteristic length"or diameter of the fluid flow (m)

μ = the viscosity of the fluid

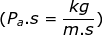
For a circular pipe, the characteristic length is the diameter of the pipe. The boundaries between the types of flow are:

Reynold's Number Formula Questions:

1) A person turns on the cold water tap in their kitchen. Water flows to the tap through a copper pipe 6.00 mm diameter at a velocity of 1.00 m/s. The density of the water in the pipe is 1000 kg/m³, and its viscosity is 0.00133 Pa∙s. What is the Reynold's number, and what kind of flow is occurring in the pipe?

Answer:

The diameter of the pipe is 6.00 mm, which is equal to 0.00600 m. The Reynold's number can be found from the formula: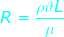

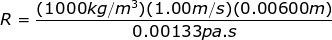
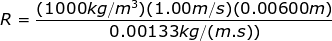
R = 4511

The Reynold's number is R = 4511. This number is greater than 4000, which means it is in the range that indicates turbulent flow. The flow through the copper pipe going to the tap is turbulent.

2) The viscosity of liquid honey near room temperature is 10.0Pa∙s, and it has a density of 1360 kg/m³. At a honey bottling plant, honey is flowing through a 10.0 cm diameter pipe at a velocity of 2.00 m/s. What is the Reynold's number, and what kind of flow is occurring in the pipe? The viscosity of honey changes significantly if the temperature is changed. If the temperature of the honey is raised, and the viscosity becomes 0.0200 Pa∙s, what is the Reynold's number, and what kind of flow would occur in the pipe?

Answer:

The diameter of the pipe is 10.0 cm, which is equal to 0.100 m. The Reynold's number for room-temperature honey (viscosity μ = 10.0Pa∙s) can be found from the formula: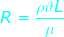

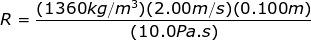
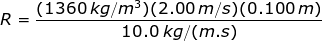
R = 27.2

The Reynold's number is R = 27.2. This number is much less than 2300, which means it is in the range that indicates laminar flow. For room-temperature honey in this pipe, the flow is laminar

For higher-temperature honey, with viscosity 0.0200Pa∙s, the Reynold's number is:

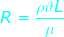
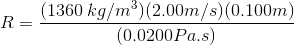
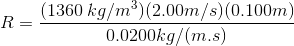
R = 13600

The Reynold's number is R = 13600. This number is much greaterthan 4000, which means it is in the range that indicates turbulent flow. In this situation, the flow of the honey through the pipe is turbulent.