Speed of sound Formula

The speed of sound is the dynamic propagation of sound waves. The speed or dynamic of the propagation of the sound wave depends on the characteristics of the medium in which the propagation takes place and not on the characteristics of the wave or the force that generates it. Its propagation in a medium can be used to study some properties of this transmission medium.

In gases the equation of the speed of sound is:

speed of sound = the square root of (the coefficient of adiabatic expansion * the pressure of the gas / the density of the medium).

The equation is:

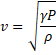
We have:

v = speed of sound.

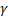= the coefficient of adiabatic expansion.

P = the pressure of the gas.

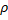= the density of the medium.

Speed of sound Questions:

1)What is the speed of sound in a helium gas at a pressure of 150000 Pa?

Answer: The first thing is to look for the values of the adiabatic expansion coefficient and helium density.

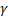= 1.66

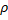= 0.1664 kg/m³

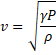= (1.66*150000Pa/0.1664 kg/m³)^-1/2 = 1223.27193656 m/s

v = 1223.27193656 m/s

2)At what pressure is an argon gas found, if the sound travels with a velocity of 1000 m/s through it?

Answer: The first thing is to look for the values of the adiabatic expansion coefficient and helium density.

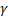= 1.76

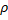= 1.78 kg/m³

P = (v² * 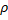) / 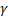= ((1000m/s)²*1.78kg/m³)/1.76 = 1011363.64 Pa

P = 1011363.64 Pa