Torque Formula (Moment of Inertia and Angular Acceleration)

In rotational motion, torque is required to produce an angular acceleration of an object. The amount of torque required to produce an angular acceleration depends on the distribution of the mass of the object. The moment of inertia is a value that describes the distribution. It can be found by integrating over the mass of all parts of the object and their distances to the center of rotation, but it is also possible to look up the moments of inertia for common shapes. The torque on a given axis is the product of the moment of inertia and the angular acceleration. The units of torque are Newton-meters (N∙m).

torque = (moment of inertia)(angular acceleration)

τ = Iα

τ = torque, around a defined axis (N∙m)

I = moment of inertia (kg∙m²)

α = angular acceleration (radians/s²)

Torque Formula Questions:

1) The moment of inertia of a solid disc is 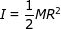, where M is the mass of the disc, and R is the radius. The wheels of a toy car each have a mass of 0.100 kg, and radius 20.0 cm. If the angular acceleration of a wheel is 1.00 radians/s², what is the torque?

Answer: The torque can be found using the torque formula, and the moment of inertia of a solid disc. The torque is:

τ = Iα

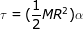
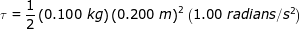
τ = 0.0020 N∙m

The torque applied to one wheel is 0.0020 N∙m.

2) The moment of inertia of a thin rod, spinning on an axis through its center, is 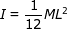, where M is the mass and L is the length of the rod. Assume a helicopter blade is a thin rod, with a mass of 150.0 kg and a length of 8.00 m. To achieve an angular acceleration of 18.00 radians/s², what torque is required?

Answer: The torque can be found using the torque formula, and the moment of inertia of a thin rod. The torque is:

τ = Iα

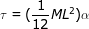
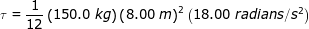
τ = 14 400 N∙m

The torque required is 14 400 N∙m.