Vector Projection Formula
A vector is a mathematical entity. It is represented by a line segment that has module (the length of the segment), direction (the line where the segment is represented) and direction (the orientation of the segment, from the origin to the end of the vector). A unit vector is a vector of module one, which is given by the vector divided by its module.
The vector projection of a vector on a vector other than zero b (also known as vector component or vector resolution of a in the direction of b) is the orthogonal projection of a on a straight line parallel to b. The vector projection of a vector on a vector other than zero b (also known as vector component or vector resolution of a in the direction of b) is the orthogonal projection of a on a straight line parallel to b. It is a parallel vector a b, defined as the scalar projection of a on b in the direction of b.
Projection of the vector a on the vector b = product scale between vectors a and b /( vector module b)^2
The equation is written
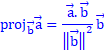
We have:
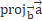 = Projection of the vector a on the vector b
= Projection of the vector a on the vector b
 = vector a
= vector a
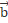 = vector b
= vector b
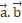 = product scale between vectors a and b
= product scale between vectors a and b
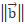 = module of vector b
= module of vector b
Vector projection Questions:
1) Find the vector projection of vector  = (3,4) onto vector
= (3,4) onto vector 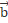 = (5,−12).
= (5,−12).
Answer: First, we will calculate the module of vector b, then the scalar product between vectors a and b to apply the vector projection formula described above.
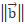 =
= 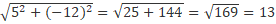
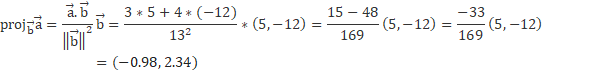
2) Find the vector projection of vector 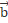 = (2,-3) onto vector
= (2,-3) onto vector  = (-7,1).
= (-7,1).
Answer: First, we will calculate the module of vector a, then the scalar product between vectors a and b to apply the vector projection formula described above.
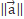 =
= 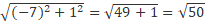
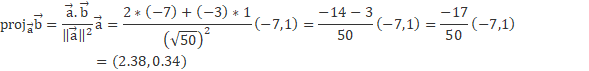
|
Related Links: |
