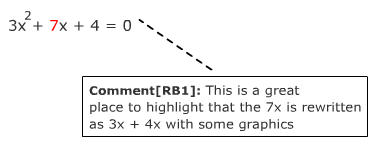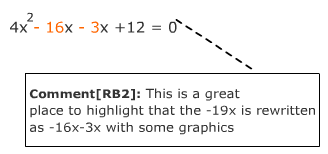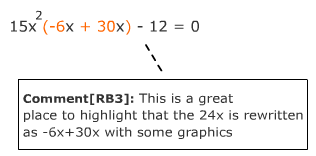Factoring Quadratic Equations when a ≠ 1

Step 1: Write the equation in the general form

ax² + bx + c = 0.

This equation is already in the proper form where a = 3, b = 7 and c = 4.

3x² + 7x + 4 = 0

Step 2: Multiple a · c and find the factors of the result, let's call this p.

a = 3, c = 4

3 · 4 = 12 = p

Step 3: Determine the factor pairs of p that will add to b.

3.1: List the factor pairs of p.

First ask yourself what are the factors pairs of p, ignoring the negative sign for now.

3.2: Determine the signs of the factors.

If p is positive then both factors will be positive or both factors will be negative.

If p is negative then one factor will be positive and the other negative.

3.3: Determine the factor pair that will add to give b.

If both p and b are positive, both factors will be positive.

If both p and b are negative, the larger factor will be negative and the smaller will be positive.

If p is positive and b is negative, both factors will be negative.

If p is negative and b is positive, the larger factor will be positive and the smaller will be negative.

3.1: Factors pairs of 12:

(1, 12);(2, 6);(3, 4)

3.2: p = 12, a positive number, therefore both factors will be positive or both factors will be negative.

3.3: b = 7, a positive number, therefore both factors will be positive.

$\left(1,12\right): 12+1=13\ne b$

$\left(2,6\right): 2+6=8\ne b$

These pairs do not work.

$\left(3,4\right): 3+4=7= b$

This pair works!!!

(3, 4)

Step 4: Rewrite bx as a sum of two x-terms using the factor pair found in Step 3.

3x² + 3x + 4x + 4 = 0

Step 5: Group the terms for factoring.

(3x² + 3x) + (4x + 4) = 0

Step 6: Factor the greatest common denominator from each group.

3x(x + 1) + 4(x + 1) = 0

Step 7: Rewrite the equation as two polynomial factors.

Notice that the parenthetical expression is the same for both groups. If this does not occur, regroup the terms and try again.

Using the reverse of the distributive property we can write the outside expressions (shown in red in Step 6) as a second polynomial factor.

(3x + 4)(x + 1) = 0

Step 8: Set each factor to zero and solve for x.

(3x + 4) = 0, or (x + 1) = 0

$x=-\frac{4}{3}$, or x = -1

Step 1: Write the equation in the general form

ax² + bx + c = 0.

This equation is already in the proper form where a = 4, b = -19 and c = 12.

4x² - 19x + 12 = 0

Step 2: Multiple a · c and find the factors of the result, let's call this p.

a = 4, c = 12

4 · 12 = 48 = p

Step 3: Determine the factor pairs of p that will add to b.

3.1: List the factor pairs of p.

First ask yourself what are the factors pairs of p, ignoring the negative sign for now.

3.2: Determine the signs of the factors.

If p is positive then both factors will be positive or both factors will be negative.

If p is negative then one factor will be positive and the other negative.

3.3: Determine the factor pair that will add to give b.

If both p and b are positive, both factors will be positive.

If both p and b are negative, the larger factor will be negative and the smaller will be positive.

If p is positive and b is negative, both factors will be negative.

If p is negative andb is positive, the larger factor will be positive and the smaller will be negative.

3.1: Factors pairs of 48:

(1, 48);(2, 24);(3, 16);(4, 12);(6, 8)

3.2: p = 48, a positive number, therefore both factors will be positive or both factors will be negative.

3.3: b = -19, a negative number, therefore both factors will be negative.

$\left(-1,-48\right): -1-48=-49\ne b$

$\left(-2,-24\right): -2-24=-26\ne b$

$\left(-4,-12\right): -4-12=-16\ne b$

$\left(-6,-8\right): -6-8=-14\ne b$

These pairs do not work.

$\left(-3,-16\right): -3-16=-19= b$

This pair works!!!

(-3, -16)

Step 4: Rewrite bx as a sum of two x-terms using the factor pair found in Step 3.

4x² - 19x + 12 = 0

Step 5: Group the terms for factoring.

(4x² -16x) + (-3x + 12) = 0

Step 6: Factor the greatest common denominator from each group.

4x(x - 4) - 3(x - 4) = 0

Step 7: Rewrite the equation as two polynomial factors.

Notice that the parenthetical expression is the same for both groups. If this does not occur, regroup the terms and try again.

Using the reverse of the distributive property we can write the outside expressions (shown in red in Step 6) as a second polynomial factor.

(4x - 3)(x - 4) = 0

Step 8: Set each factor to zero and solve for x.

(4x - 3) = 0, or (x - 4) = 0

$x=\frac{3}{4}$ , or x = 4

Step 1: Write the equation in the general form ax² + bx + c = 0.

This equation is already in the proper form where a = 15, b = 24 and c = -12.

15x² + 24x - 12 = 0

Step 2: Multiple a · c and find the factors of the result, let's call this p.

a = 15, c = -12

15 · (-12) = -180 = p

Step 3: Determine the factor pairs of p that will add to b.

3.1: List the factor pairs of p.

First ask yourself what are the factors pairs of p, ignoring the negative sign for now.

3.2: Determine the signs of the factors.

If p is positive then both factors will be positive or both factors will be negative.

If p is negative then one factor will be positive and the other negative.

3.3: Determine the factor pair that will add to give b.

If both p and b are positive, both factors will be positive.

If both p and b are negative, the larger factor will be negative and the smaller will be positive.

If p is positive and b is negative, both factors will be negative.

If p is negative and b is positive, the larger factor will be positive and the smaller will be negative.

3.1: Factors pairs of 180:

(1,180);(2,90);(3,60);(4,45);(5,36);(6,30);

(9,20);(10,18);(12,15)

3.2: p = -180, a negative number, therefore one factor will be positive and the other negative.

3.3: b = 24, a positive number, therefore the larger factor will be positive and the smaller will be negative.

$\left(-1,-80\right): -1+180=179\ne b$

$\left(-2,-0\right): -2+90=88\ne b$

$\left(-3,60\right): -3+60=57\ne b$

$\left(-4,45\right): -4+45=41\ne b$

$\left(-5,-6\right): -5+36=31\ne b$

$\left(-9,20\right): -9+20=11\ne b$

$\left(-10,18\right): -1+18=8\ne b$

These pairs do not work.

$\left(-6,-0\right): -6+30=24= b$

This pair works!!!

(-6, 30)

Step 4: Rewrite bx as a sum of two x-terms using the factor pair found in Step 3.

15x² + 24x - 12 = 0

Step 5: Group the terms for factoring.

Grouping 1:

(15x² -6x) + (30x - 12) = 0

OR

Grouping 2:

(15x² + 30x) +(-6x + 12) = 0

Step 6: Factor the greatest common denominator from each group.

Grouping 1:

3x(5x - 2) + 6(5x - 2) = 0

OR

Grouping 2:

15x(x + 2) - 6(x - 2) = 0

Step 7: Rewrite the equation as two polynomial factors.

Notice that the parenthetical expression is the same for both groups. If this does not occur, regroup the terms and try again.

Using the reverse of the distributive property we can write the outside expressions (shown in red in Step 6) as a second polynomial factor.

Grouping 1:

(3x + 6)(5x - 2) = 0

Grouping 2:

(15x - 6)(x + 2) = 0

Step 8: Set each factor to zero and solve for x.

Grouping 1:

(3x + 6) = 0, or (5x - 2) = 0

$x=-\frac{6}{3}=-2$ , or $x=\frac{2}{5}$

Grouping 2:

(15x - 6) = 0, or (x + 2) = 0

$x=\frac{6}{15}=\frac{2}{5}$ , or x = -2

In either case the answer is the same.