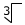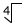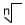Radical Expressions
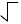 " symbol is called the radical symbol. When a number is added under the radical symbol, for instance, , it becomes a radical expression.
can be read as "the square root of 16", "root 16" or "radical 16".
" symbol is called the radical symbol. When a number is added under the radical symbol, for instance, , it becomes a radical expression.
can be read as "the square root of 16", "root 16" or "radical 16".Each radical expression has an index and a radicand.
The square root is the most popular radical. For instance has a radicand of 9 and index of 2. However, it is written as and the index of two is understood. "Squaring" a number and "taking the square root" are opposite operations.
Numbers can be raised to powers other than two. For instance numbers can be cubed (raised to the 3rd power), and raised to the 4th, 5th , 6th and so on........ In the same way numbers can have different "roots".
|
Radical |
Read as |
Example |
Opposite Operation |
|
|
Square root |
|
52 = 25 |
|
|
Cube root |
|
23= 8 |
|
|
Fourth root |
|
34 = 81 |
|
|
nth root |
Used to indicate "any" root |
|
Radical expression |
Simplified answer |
Perfect/Non-Perfect |
|
|
6 because 62 = 36 |
Perfect square |
|
|
3 because 33 = 27 |
Perfect cube |
|
|
answer in radical form 2.6 approximate answer |
Non-Perfect |
To link to this Radical Expressions page, copy the following code to your site: