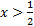Solving Multi-Step Inequalities
1)You reverse the sides of the equation
or
2)You multiply or divide both sides by a negative number.
or
2)You multiply or divide both sides by a negative number.
Examples:
1) 3x - 4 < 5
3x - 4 + 4 < 5 + 4
3x < 9
3x - 4 + 4 < 5 + 4
3x < 9
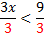
x < 3The symbol is never switched.
2) 2(x - 3) - 4x > 8
2x - 6 - 4x > 8
-2x - 6 > 8
-2x - 6 + 6 > 8 + 6 Notice the symbol does not switch here because we are adding.
-2x > 14
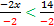The symbol switches because we are dividing by a negative number.
x < -7
3)2y - 8≤6y + 4
2y-6y- 8 ≤ 6y - 6y + 4
2y - 6y - 8≤ 4
-4y - 8≤ 4
-4y - 8 + 8≤ 4 + 8
-4y ≤ 12
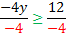
y ≥ - 3 Notice the symbol only switched when we divided by a negative number
2x - 6 - 4x > 8
-2x - 6 > 8
-2x - 6 + 6 > 8 + 6 Notice the symbol does not switch here because we are adding.
-2x > 14
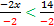The symbol switches because we are dividing by a negative number.x < -7
3)2y - 8≤6y + 4
2y-6y- 8 ≤ 6y - 6y + 4
2y - 6y - 8≤ 4
-4y - 8≤ 4
-4y - 8 + 8≤ 4 + 8
-4y ≤ 12
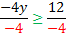
y ≥ - 3 Notice the symbol only switched when we divided by a negative number
Practice: Solve the following inequalities.
1) -5x + 1 ≤ 4
2) 3y + 6y + 1 > - 8
3) 2(x - 4) + 3x < 6
4) 3y + 1 ≥ 8y - 4
5) - 3x + 5x - 2 > - 4x + 1
2) 3y + 6y + 1 > - 8
3) 2(x - 4) + 3x < 6
4) 3y + 1 ≥ 8y - 4
5) - 3x + 5x - 2 > - 4x + 1
Answers:1)
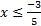2) y > - 13)
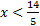4) y ≤ 15)