Home > Math > Calculus > Extreme Value Theorem

Extreme Value Theorem

The first derivative can be used to find the relative minimum and relative maximum values of a function over an open interval. These values are often called extreme values or extrema (plural form).

A point is considered a minimum point if the value of the function at that point is less than the function values for all x-values in the interval.

Conversely, a point is considered a maximum point if the value of the function at that point is greater than the function values for all x-values in the interval.

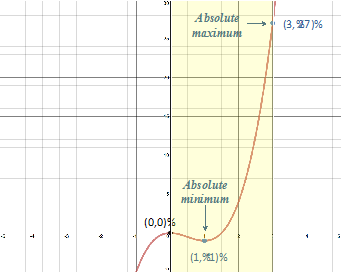
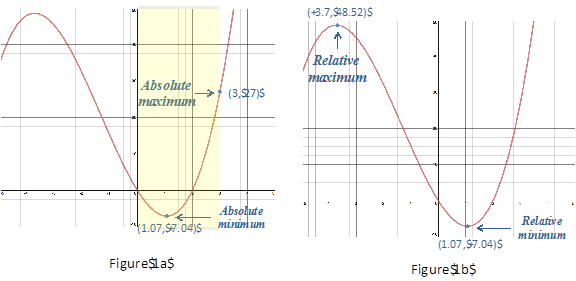
Look at the graph of f(x) = x3 + 4x2 - 12x over the interval [0, 3], Figure 1a. From the graph you can see that is has a maximum at (3, 27) and a minimum at (1.07, -7.04). On a closed interval these points are referred to as absolute or global minimum/maximum points.

EXTREME VALUE THEOREM:


If a function is continuous on a closed interval, the function has both a minimum and a maximum.



If you look at this same graph over the entire domain you will notice that there is no absolute minimum or maximum value.

However, there are minimum and maximum points where the hills in the graph reach their highest (-3.7, 48.52) or lowest point (1.07, -7.04). These points are called relative or local minimum/maximum points.



Because relative minimums/maximums occur at the top or valley of a hill, the slope at these points is either zero or undefined. The x-values at these points are called critical numbers. The critical numbers of f(x) = x3 + 4x2 - 12x are -3.7, 1.07.

Thus the extrema on a closed interval can be determine using the first derivative and these guidleines.

GUIDELINES FOR FINDING EXTREMA FOR A CLOSED INTERVAL:


To find the extrema for the function f over the closed interval [a, b]:

1. Find the critical numbers of f in (a, b).

2. Evaluate f at each critical number found in Step 1 over (a, b).

3. Evaluate f at each end point of the interval [a, b].

4. The least of these values is the minimum and the greatest is the maximum.

Let's look at a couple examples.

Example 1: Find the extrema of f(x) = 2x3 - 3x2 on the interval [0, 3]

Step 1: Find the critical numbers of f(x) over the open interval (a, b).


Find the first derivative and evaluate it for f ′( x )=0 or f ′( x ) does not exist.

f(x) = 2x3 - 3x2 Original function


f ′ ( x )=6 x 2 −6x f ′( x )


0 = 6x2 - 6x  Set f′( x )=0


0 = 6x(x - 1) Factor out 6x


6x = 0; x = 0   Set factors to 0


x - 1 = 0; x = 1 Solve for x


f ′( x ) will always exist therefore all the critical numbers have been found.


Critical numbers are: {0, 1}

Step 2: Evaluate f(x) at each critical number.

f( 0 )=2 ( 0 ) 3 −3 ( 0 ) 2 =0  f(0) = 0


f( 1 )=2 ( 1 ) 3 −3 ( 1 ) 2 =−1 f(1) = -1

Step 3: Evaluate f(x) at each end point over the closed interval [a, b].

f(0) = 0 f(0) = 0


f( 3 )=2 ( 3 ) 3 −3 ( 3 ) 2 =27 f(3) = 27

Step 4: The least of these values is the minimum and the greatest is the maximum.


Left endpoint

Critical Number

Critical Number

Right Endpoint

f(0) = 0

f(0) = 0

f(1) = -1

Minimum

f(3) = 27

Maximum


Example 2: Find the extrema of f(x) = 3x - 4x3 on the interval [0, 2]

Step 1: Find the critical point over the open interval of (a, b).


Find the first derivative and evaluate it for f′( x )=0 or f′( x ) does not exist.

f(x) = 3x - 4x3 Original function


f ′ ( x )=3−12 x 2 f′( x )


0 = 3 - 12x2 Set f′( x )=0


0 = 3(1 - 4x2)  Factor out 3


0 = 3(1 - 2x)(1 + 2x)  Factor quadratic


1−2x=0;x= 1 2     Set factors to 0


1+2x=0;x=− 1 2  Solve for x


f′( x ) will always exist therefore all the critical numbers have been found.


Critical numbers are: { 1.2, − 1 2 }

Step 2: Evaluate f(x) at each critical number.

f( 1 2 )=3( 1 2 )−4 ( 1 2 ) 3 =1    f( 1 2 )=1


f( − 1 2 )=3( − 1 2 )−4 ( − 1 2 ) 3 =−1 f( − 1 2 )=−1

Step 3: Evaluate f(x) at each end point over the closed interval [a, b].

f( 0 )=3( 0 )−4 ( 0 ) 3 =0      f(0) = 0


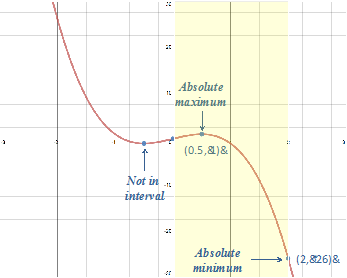
f( 2 )=3( 2 )−4 ( 2 ) 3 =−26   f(2) = -26

Step 4: The least of these values is the minimum and the greatest is the maximum.


Left endpoint

Critical Number

Critical Number

Right Endpoint

f(0) = 0

f( − 1 2 )=−1

f( 1 2 )=1

Maximum

f(2) = -26

Minimum






Related Links:
Math
algebra
Even and Odd Functions
Function Transformations
Calculus Topics


To link to this Extreme Value Theorem page, copy the following code to your site: