Besides SSS (Side, Side, Side), there are several other ways to show that two triangles are congruent. Let's take a look at more.

Method 2: ASA (Angle, Side, Angle)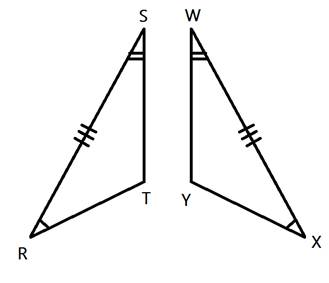



You can also prove that two triangles are congruent by showing that two angles and the included side are congruent. In this example, < R is congruent to < X, < S is congruent to < W and side RS is congruent to side XW.

(Note that the side must be between the two angles.)

Let's take a look at how to use this congruence in a proof.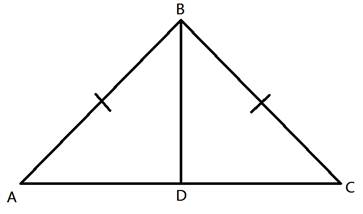



Given: 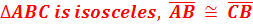< ABD ≅ < CBD

Prove: D is the midpoint of AC

First let's determine what we know. We have been given a pair of congruent angles and a pair of congruent sides. We also know that the larger triangle around the outside is isosceles. How does that help us? Because the triangle is isosceles, we know that it has two congruent sides and two congruent angles. So we can say that < A is congruent to < C.

Let's show this in the table:

Statements	Reasons
1. < ABD ≅ < CBD ≅ CD	1. Given
2. AB ≅ CB	2. Given
3. ΔABC is isosceles	3. Given
4. < A ≅ < C	4. Definition of isosceles triangle

Now we have show that an angle, a side and another angle are congruent in each triangle. So that means by ASA (Angle, Side, Angle Congruence) we can show that ΔABD and ΔCBD are congruent. And therefore, their corresponding parts are also congruent.

Statements	Reasons
1. < ABD ≅ < CBD ≅ CD	1. Given
2. AB ≅ CB	2. Given
3. ΔABC is isosceles	3. Given
4. < A ≅ < C	4. Definition of isosceles triangle
5. ΔABD ≅ ΔCBD	5. ASA
6. AD ≅ CD	6. CPCTC

(Note: We used that crazy CPCTC reason again. If you forgot, it stands for "Corresponding Parts of Congruent Triangles are Congruent." Once you show that two triangles are congruent you can use this reason to show that any of the corresponding sides or corresponding angles are congruent as well.)

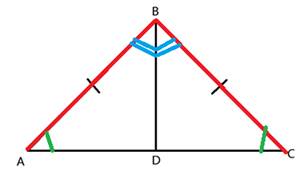
Here we have shown that the two pieces on the bottom are equal in size. That means that point D is in the middle of them. And therefore, D must be the midpoint of the segment AC.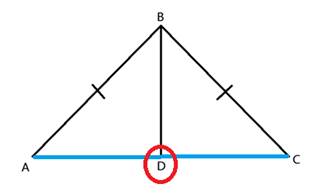

Statements	Reasons
1. < ABD ≅ < CBD ≅ CD	1. Given
2. AB ≅ CB	2. Given
3. ΔABC is isosceles	3. Given
4. < A ≅ < C	4. Definition of isosceles triangle
5. ΔABD ≅ ΔCBD	5. ASA
6. AD ≅ CD	6. CPCTC
7. D is the midpoint of AC	7. Definition of midpoint

Let's Recap!

We used given information along with definitions to show that two triangles were congruent using Angle, Side, Angle. Once the two triangles are shown to be congruent, we were able to also say that all other corresponding sides or corresponding angles are also congruent. If these additional congruent pieces do not complete the proof, be sure to use other known definitions.

Related Links: Math Geometry Triangles Congruent Triangles