You have seen how to use SSS and ASA, but there are actually several other ways to show that two triangles are congruent. Here, we will show another two methods and proofs that use it.

Method 3: SAS (Side, Angle, Side)

Similar to Method 2, we can use two pairs of congruent sides and a pair of congruent angles located between the sides to show that two triangles are congruent.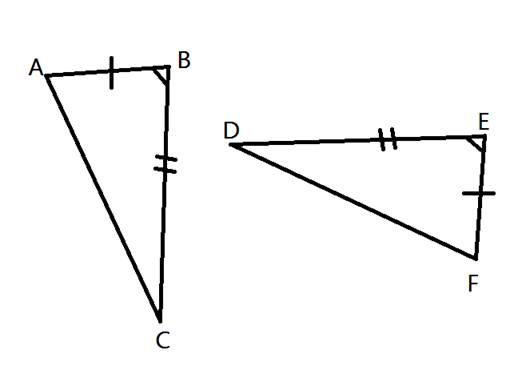



In this diagram, 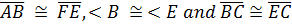. This shows that two sides and the included angle are the same in each triangle. We call this SAS or Side, Angle, Side.

We can use SAS to show that two triangles are congruent or use it to prove other possible facts about the triangles.

Here is an example:

1. Given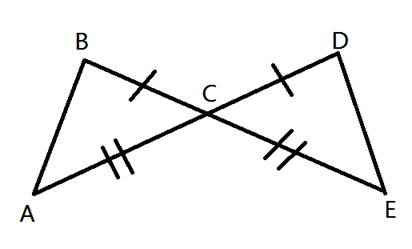



Prove that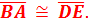

Like in other proofs, be sure to start by showing what information has been given.

Statements	Reasons
1. BC ≅ DC	1. Given
2. AC ≅ EC	2. Given

Next, use other information you can gain from the diagram. For example, we can see that < BCA and < DCE are congruent because they are vertical angles.

Statements	Reasons
1. BC ≅ DC	1. Given
2. AC ≅ EC	2. Given
3. < BCA ≅ < DCE	3. Vertical Angles

Now we have shown that each triangle has corresponding parts showing SAS or Side Angle Side. Therefore, the two triangles are congruent.

Statements	Reasons
1. BC ≅ DC	1. Given
2. AC ≅ EC	2. Given
3. < BCA ≅ < DCE	3. Vertical Angles
4. ΔABC ≅ ΔEDC	4. SAS

Finally, we can show that the other pair of corresponding sides are congruent because the triangles are congruent. Recall that the reason for this is abbreviated to CPCTC.

Statements	Reasons
1. BC ≅ DC	1. Given
2. AC ≅ EC	2. Given
3. < BCA ≅ < DCE	3. Vertical Angles
4. ΔABC ≅ ΔEDC	4. SAS
5. BA ≅ DE	5. CPCTC

Method 4: AAS (Angle, Angle, Side)

We can also show that two triangles are congruent by showing two angles and a non-included side of one triangle correspond and are congruent to two angles and a non-included side of another triangle.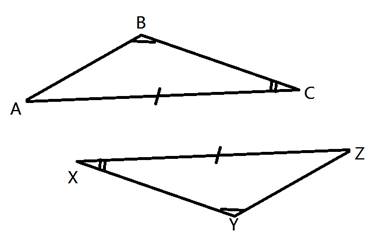



Here we can see that < B is congruent to < Y, < C is congruent to < X and AC ≅ ZX. This shows that in these two triangles two angles and a non-included side in ΔABC are congruent to two angles and a non-included side of ΔZYX. Therefore, ΔABC ≅ ΔZYX.

Here is a look at another proof using AAS.

2. Given: < AFD ≅ < CDF, < BFD ≅ < BDF, EA ≅ EC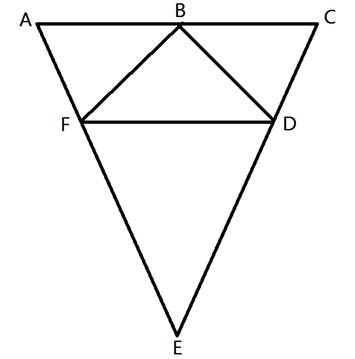



Prove: B is the midpoint of AC.

First, let's take a look at the given information.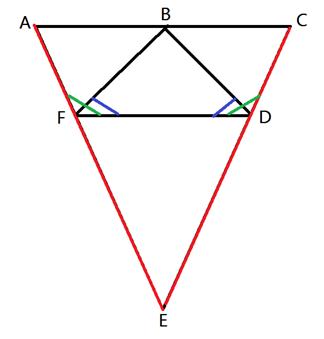


Given: < AFD ≅ < CDF, < BFD ≅ < BDF, EA ≅ EC

We need to use this information to show that ΔABF ≅ ΔCBF. Then we will be able to say that AB ≅ CB. If these two segments are congruent, then B must be the midpoint because it would be right in the middle. So the job now is to show that those two triangles are congruent.

Statements	Reasons
EA ≅ EC	Given
Δ AEC is isosceles	Definition of Isosceles
< CAE ≅ < ACE	If the sides are congruent, the angles are congruent.

First we showed that the top two angles are congruent. Next we will show that BF ≅ BD.

Statements	Reasons
EA ≅ EC	Given
Δ AEC is isosceles	Definition of Isosceles
< CAE ≅ < ACE	If the sides are congruent, the angles are congruent.
< BFD ≅ < BDF	Given
BF ≅ BD	If the angles are congruent, the sides are congruent.

So far we have a pair of corresponding congruent angles and a pair of corresponding congruent sides. Next, we can show that one more pair of corresponding angles is congruent.

Statements	Reasons
EA ≅ EC	Given
Δ AEC is isosceles	Definition of Isosceles
< CAE ≅ < ACE	If the sides are congruent, the angles are congruent.
< BFD ≅ < BDF	Given
BF ≅ BD	If the angles are congruent, the sides are congruent.
< AFD ≅ < CDF	Given
< AFB ≅ < CDB	If two congruent angles are subtracted from two congruent angles, the differences are congruent angles.

Now we have two pairs of angles and a pair of non-included sides, showing that the two triangles are congruent. We will use CPCTC to show that side AB and CB are also congruent.

Statements	Reasons
EA ≅ EC	Given
Δ AEC is isosceles	Definition of Isosceles
< CAE ≅ < ACE	If the sides are congruent, the angles are congruent.
< BFD ≅ < BDF	Given
BF ≅ BD	If the angles are congruent, the sides are congruent.
< AFD ≅ < CDF	Given
< AFB ≅ < CDB	If two congruent angles are subtracted from two congruent angles, the differences are congruent angles.
Δ ABF ≅ Δ CBF	AAS
AB ≅ CB	CPCTC
B is the midpoint of AC	Definition of midpoint

Let's Review

So far, you have seen how to use SSS, ASA, SAS, and AAS to show that two triangles are congruent. These theorems can be used to show other true facts about the given triangles. Once you have two congruent triangles, be sure to use CPCTC to show that other corresponding parts are congruent as well. You can mix in definitions of other things like isosceles triangles, midpoint, angle bisector, etc. to complete your proofs.

Related Links: Math Geometry Triangles Congruent Triangles