It is possible to prove that a quadrilateral is a rectangle. Before we get started with the proofs, let's review what is special about rectangles. First, we know that rectangles are parallelograms, so...



But there are also things that make rectangles more than just the average parallelogram.



Let's see why we can claim that the diagonals are congruent. Here is a sample proof: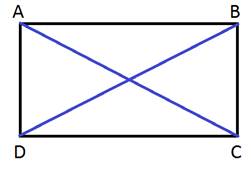



Given: Quadrilateral ABCD is a rectangle.

Prove: AC ≅ BD

Statements	Reasons
AD ≅ BC	Definition of Rectangle
DC ≅ DC	Reflexive Property
<A, <B, <C, <D are all congruent and right angles	Definition of Rectangle
ΔBCD ≅ ΔADC	Side, Angle, Side
AC ≅ BD	CPCTC

Here you can see that the two triangles on either side are congruent and therefore, the corresponding sides are congruent. This shows that for any rectangle, the diagonals will be congruent.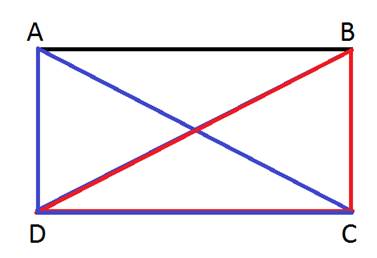



Showing that the diagonals are congruent is a great way to show that a figure is a rectangle when you already know that the figure is a parallelogram. Other ways would include showing that the shape has 4 right angles. If you already know that the shape is a parallelogram, you will only have to show that one of the angles is a right angle and then it would follow that all of the angles are right angles.

Example:

Prove that the following four points will form a rectangle when connected in order.


Step 1: Plot the points to get a visual idea of what you are working with.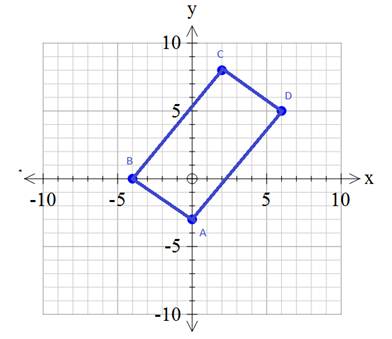



Step 2:Prove that the figure is a parallelogram.

There are 5 different ways to prove that this shape is a parallelogram. Choose one of the methods.


In this example, we will show that both pairs of opposite sides are parallel. To do this we need to calculate the slope of each side. If we can show that the slopes of the opposite sides are the same, then the opposite sides are parallel.

Recall that the slope can be determined using m =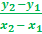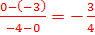

Slope of AB =

Slope of CD =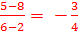

Slope of BC =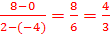

Slope of AD =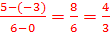

The slopes of the opposites were the same, so ABCD is a parallelogram.

Step 3: Next, prove that the parallelogram is a rectangle.

We can do this by showing that that the diagonals are congruent or by showing that one of the angles is a right angle.

It may be easier to show that one of the angles is a right angle because we have already computed all of the slopes.

We could show that AB is perpendicular to BC because the slopes are negative reciprocals of each other. 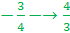And because these two segments are perpendicular, <B must be a right angle. If <B is a right angle, and the opposite angles are congruent, we get that <D is also right and then it would follow that <A and <C must also be right angles. Because the parallelogram has four right angles. ABCD must be a rectangle.

Related Links: Math Geometry Triangles Congruent Triangles