What does the Hypotenuse - Leg Theorem say?

If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

So we only have to show that in two right triangles that the hypotenuse is congruent to the other hypotenuse and show that one leg is congruent to another corresponding leg in order to show that the two triangles are congruent.

Here is an example: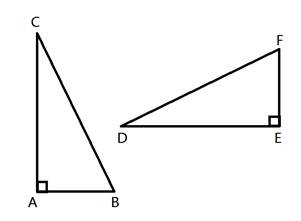



In this example, let's assume we are given that AB ≅ EF and CB ≅ DF.

Notice that both triangles are right triangles. The hypotenuse of triangle ABC is CB and the hypotenuse of triangle DEF is DF. So we can see that the hypotenuses, CB and DF, are congruent from the given statements.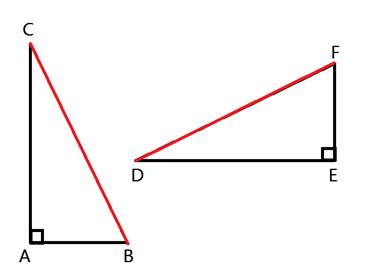



In addition, we have been told that AB is congruent with EF.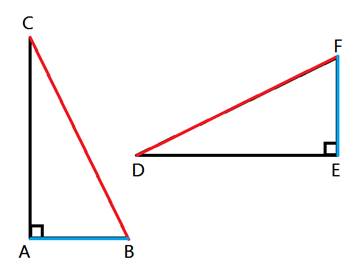



Therefore, we have two congruent triangles, with congruent hypotenuses and congruent legs, showing that these two triangles are congruent. So we can say that ΔABC ≅ ΔEFD.

The Hypotenuse - Leg theorem can be used to prove more than just congruent triangles by including the CPCTC move. Recall that CPCTC represents "corresponding parts of congruent triangles are congruent."

Here is another example: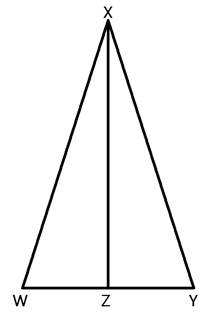



Given: <W is congruent to <Y and XZ is an altitude.

Prove: WZ is congruent to YZ.

Let's take a look at how to use Hypotenuse - Leg to complete this informal proof.

The altitude XZ is perpendicular to WY, which means that <XZW and <XZY are right angles. Therefore, both triangle XZW and triangle XZY are both right triangles. In addition, because <W is congruent to <Y, we know that triangle WXY is isosceles and therefore WX is congruent to YX. This is helpful because WX and YX are also the hypotenuses of triangles WXZ and YXZ. We also have XZ which is a leg in both triangle WXZ and triangle YXZ, and XZ is of course congruent to XZ.

Now we have a right angle in both triangles, congruent hypotenuses and congruent legs. Therefore, triangle WXZ is congruent to triangle YXZ. And because these triangles are congruent, WZ is congruent to YZ because corresponding parts of congruent triangles are congruent.

Summing it All Up
So the main point here is that if you have two right triangles and the hypotenuses are congruent and one pair of corresponding legs are congruent, then the two triangles are congruent. This can then be used to prove other things in a triangle diagram.

Related Links: Math Geometry Triangles Congruent Triangles