You might be familiar with determining the area and perimeter of two-dimensional shapes. However, it may seem like a slightly different task when presented on the coordinate plane.

Example #1

Determine the perimeter and area of the rectangle below.



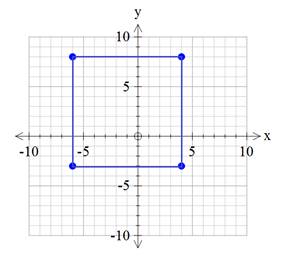
Notice that the lengths are not given. Instead, you must use the graph to determine the information.

Counting will help you to determine the lengths of the sides.



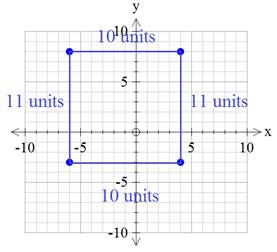
Now that you have the lengths of all the sides, you can add them to get the perimeter.

P = 10 + 10 + 11 + 11

P = 42 units

You can also use the lengths to calculate the area of the rectangle.

For a rectangle, the area is equal to the length times the width.

A = lw

A =(10 units)(11 units)

A = 110 units²

The other option, although quite tedious, would be to count all the squares inside the rectangle. If you were to do so, you would notice that there are 110 squares. Therefore, the area is 110 square units.

Example #2



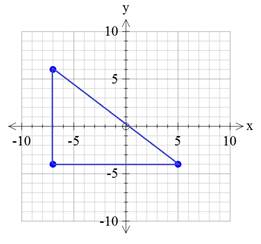
In this case, be sure to count the lengths and not actual squares when determining the lengths of each side.



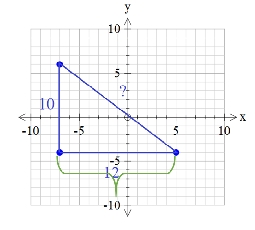
Even though 12 whole squares do not fit across the base of the triangle, there are 12 lengths.

It is impossible to determine the length of the longest side from the graph. This is one of the downfalls to being given the information on a coordinate plane. The Pythagorean Theorem can be used to calculate the third side. (Remember that the longest side must be labeled as c in the formula a² + b² = c².)

a² + b² = c²

12² + 10² = c²

144 + 100 = c²

244 = c²

√244 = c

15.6 ≈ c

This is the approximate length of the third side of the triangle.

Now we can determine the approximate perimeter of the triangle.

P = 10 + 12 + 15.6

P = 37.6 units

For the area, we can use the formula A = ½ bh. Be sure to use the
base and height that meet at a right angle.

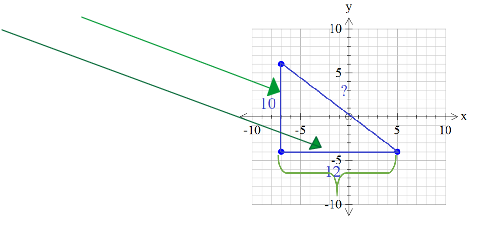
A = ½ bh

A = ½ (12 units)(10 units)

A = 60 units²

Example #3 Determine the perimeter and area of the irregular figure.



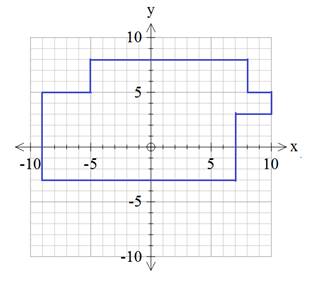
Start with the perimeter. First, determine the lengths of all the pieces.



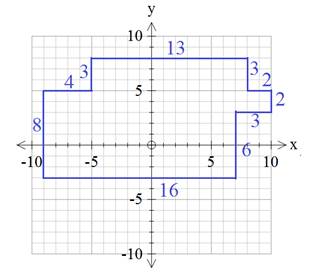
Then add the lengths together to get the perimeter.

P = 8 + 4 + 3 + 13 + 3 + 2 + 2 + 3 + 6 + 16

P = 60 units

For the area, start by chopping up the figure into rectangles. This shape can be divided up many different ways. Here is one possibility.



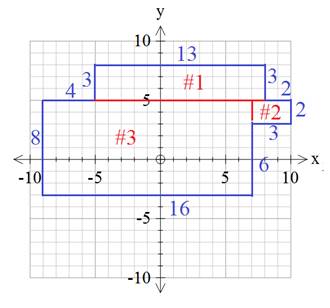
Rectangle #1

A = lw

A = (13 units)(3 units)

A = 39 units²

Rectangle #2

A = lw

A = (3 units)(2 units)

A = 6 units²

Rectangle #3

A = lw

A = (16 units)(8 units)

A = 128 units²

Next, add the areas of all the pieces to get the total area of the shape.

Total Area = 39 + 6 + 128

Total Area = 173 units²

Let's Review

When two-dimensional figures are shown on the coordinate plane, a mix of counting and the Pythagorean Theorem can be used to determine the lengths of each side. Then add up the lengths to determine the perimeter or use the basic area formulas for triangles and rectangles to determine the area of the figure.

Related Links: Math Geometry Area of a Circle Perimeter of Parallelogram