Complementary Angles
The definition of complementary angles is two angles whose sum is 90°. Simply put, if you can add the measures of two angles together and the sum is equal 90° then the angles are complementary.
We are going to look at two types of complementary angles: adjacent and non-adjacent.
Adjacent: the angles share a common side and vertex and are "side-by-side".
Example 1:
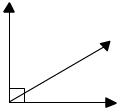
We have divided the right angle into 2 angles that are "adjacent" to each other creating a pair of adjacent, complementary angles.
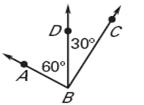
Example 2: 60°+30° = 90° complementary and adjacent
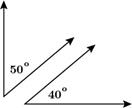
Example 3: 50°+40° = 90° complementary and non-adjacent (the angles do not share a common side).
Example 4: Given m 1 = 43° and the m
1 = 43° and the m  2 = 47° determine if the two angles are complementary.
2 = 47° determine if the two angles are complementary.
43° + 47° = 90° therefore they are complementary.
Geometry & Algebra: solve for x then find m ABD and m
ABD and m  DBC.
DBC.
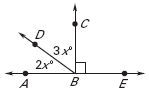
 ABD and
ABD and  DBC form a right angle therefore, they are complementary and their sum is 90°.
DBC form a right angle therefore, they are complementary and their sum is 90°.
Write an equation 2x + 3x = 90
Combine like terms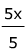 =
=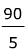
Divide both sides by 5
x = 18°
m ABD = 2x
ABD = 2x
Substitute 18 for x m ABD = 2(18°) = 36°
ABD = 2(18°) = 36°
m DBC = 3x
DBC = 3x
Substitute 18 for x m DBC = 3(18°) = 54°
DBC = 3(18°) = 54°
Check your answer 36° + 54° = 90°
A quick summary. if m 1 + m
1 + m  2 = 90° then the angles are complementary. The angle pair can either be adjacent (side- by side) or non-adjacent.
2 = 90° then the angles are complementary. The angle pair can either be adjacent (side- by side) or non-adjacent.
We are going to look at two types of complementary angles: adjacent and non-adjacent.
Adjacent: the angles share a common side and vertex and are "side-by-side".
Example 1:

We have divided the right angle into 2 angles that are "adjacent" to each other creating a pair of adjacent, complementary angles.
Example 2: 60°+30° = 90° complementary and adjacent

Example 3: 50°+40° = 90° complementary and non-adjacent (the angles do not share a common side).

Example 4: Given m
 1 = 43° and the m
1 = 43° and the m  2 = 47° determine if the two angles are complementary.
2 = 47° determine if the two angles are complementary.43° + 47° = 90° therefore they are complementary.
Geometry & Algebra: solve for x then find m
 ABD and m
ABD and m  DBC.
DBC.
 ABD and
ABD and  DBC form a right angle therefore, they are complementary and their sum is 90°.
DBC form a right angle therefore, they are complementary and their sum is 90°.Write an equation 2x + 3x = 90
Combine like terms
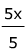 =
=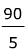
Divide both sides by 5
x = 18°
m
 ABD = 2x
ABD = 2xSubstitute 18 for x m
 ABD = 2(18°) = 36°
ABD = 2(18°) = 36°m
 DBC = 3x
DBC = 3xSubstitute 18 for x m
 DBC = 3(18°) = 54°
DBC = 3(18°) = 54°Check your answer 36° + 54° = 90°
A quick summary. if m
 1 + m
1 + m  2 = 90° then the angles are complementary. The angle pair can either be adjacent (side- by side) or non-adjacent.
2 = 90° then the angles are complementary. The angle pair can either be adjacent (side- by side) or non-adjacent.|
Related Links: Math Geometry Topics Complementary or Supplementary Polygons |
To link to this Complementary Angles page, copy the following code to your site:
