You might already know that all the angles in a rectangle are ninety degrees.



From here we can see that 4(90°) = 360°. In other words, a quadrilateral has a total of 360°.

We can use this fact to determine the missing angle in any quadrilateral or four sided shape. Here are some examples.

Example 1:



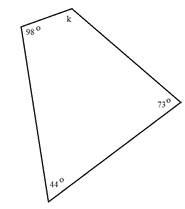
We have been given three angles and need to determine the measure of the fourth.

Step 1: Add together the measures of the known angles.

98° + 44° + 73° = 215°

Step 2: Subtract the sum from 360° to determine what remains for the fourth angle.

360° - 215° = 145°

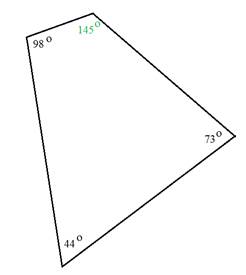
The measure of the unknown angle is 145°.



Example 2:



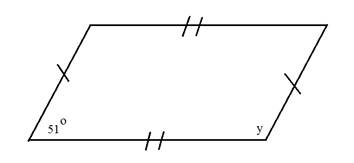
Here we have a parallelogram. The great thing about parallelograms is that the two consecutive angles must be supplementary. So we do not need to use the other angles in the figure.

Recall that supplementary angles have a sum of 180°.

Step 1: Subtract the known angle from 180°.

180° - 51° = 129°

The missing angle is 129°.

Step 2: Let's check our work. The opposite angles in a parallelogram are congruent. So there would be 2 angles that measure 51° and two angles that measure 129°.



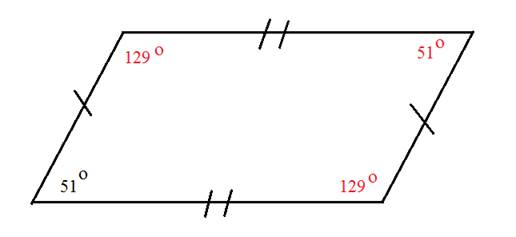
51° + 51° + 129° + 129° = 360°

Here we can see that if the missing angle is 129° that the sum of all four angles would be 360°.

Example 3:



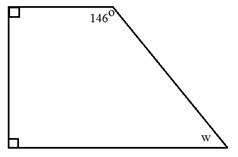
Here we have a trapezoid. The boxes in the corner tell us that those angles are right angles and they measure 90°.

Step 1:: Add together the measures of the known angles.

90° + 90° + 146° = 326°

Step 2:: Subtract the sum from 360°.

360° - 326° = 34°

The measure of angle w is 34°.



Let's Review

Quadrilaterals have 360°. Use this along with other information about the figure to determine the measure of the missing angle. If you have a rectangle or square, each of the angles measures 90°. If you have a parallelogram or rhombus, the opposite angles are the same and the consecutive angles are supplementary. For other types of quadrilaterals you may need to add the given angles and then subtract from 360°.

Related Links: Math Geometry Quadrilateral Angles Quadrilateral Shapes