It may seem easy to find the area of a rectangle, but what if the figure has more than 4 sides?



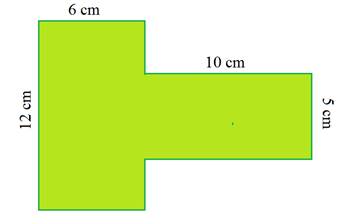
Notice that this shape has 8 sides. Therefore, we could call it an octagon.

However, a memorized formula for an irregular octagon would not be very helpful in this situation. Instead, break down the shape into rectangles.



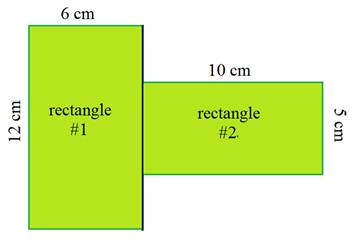
Next, calculate the area of both rectangles and add them together.



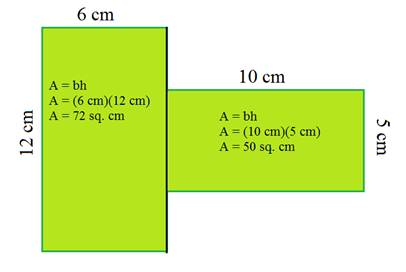
The area of the first rectangle is 72 square centimeters and the area of the second rectangle is 50 square centimeters.

Together there are 72 + 50 = 122 square centimeters.

Therefore, the area of the entire figure is 122 square centimeters.

Sometimes adding up the pieces is the easiest method. Other times you might want to take a different approach. Check out the next example.



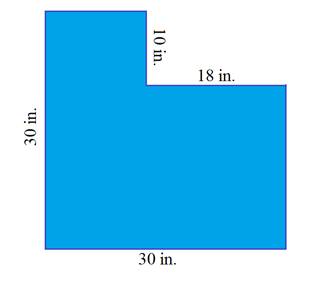
Notice that this figure looks like a square that is missing a piece.



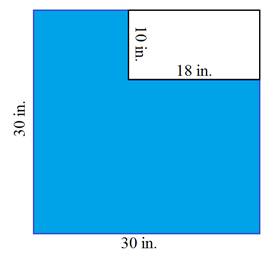
In this case, calculate the area of the square and the rectangle and then subtract.

A_square = s²        A = bh

A = (30 in.)²       A = (18 in.)(10 in.)

A = 900 in.²        A = 180 in.²

The area of the blue hexagon is 900 in.² - 180 in.² = 720 in.².

By either adding the areas or subtracting the areas of rectangles the area of an irregular shape can be calculated. This will not work for all irregular figures. You may have to use triangles or other shapes as well.



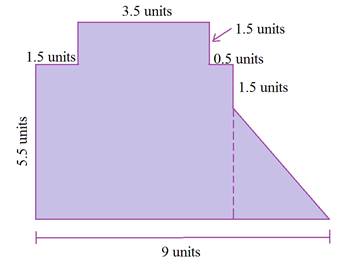
Start by breaking this figure into rectangles and triangles. There is more than one right way to do this. Here is one possible option:



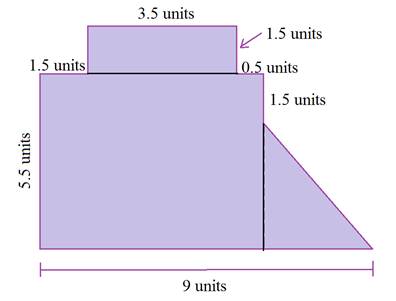
Then use the known side lengths to determine any side lengths that are still needed to calculate the area of the three pieces.


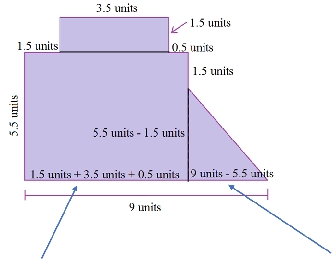
Here we added all the pieces from the top lengths. Then we can subtract this from the total of 9 units to get the base of the triangle.

Now all of the bases and heights are labeled so that the areas can be calculated.



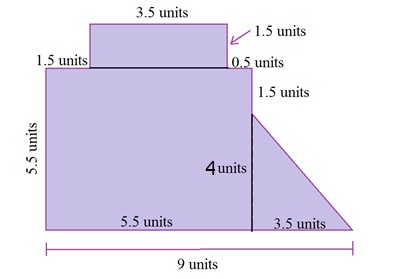
A _{top rectangle} = bh                A _{large rectangle} = bh              A _triangle = 1/2 bh

A = (3.5 units)(1.5 units)      A = (5.5 units)(5.5 units)      A = 1/2 (3.5 units)(4 units)

A = 5.25 units²                     A = 30.25 units²                  A = 7 units²

Total Area = 5.25 units² + 30.25 units² + 7 units²

Total Area = 42.5 units²

Here is one last example:



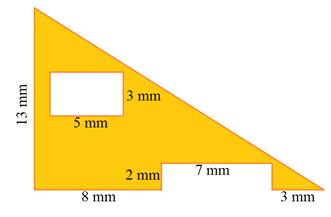
Think of this example as a triangle with two rectangles removed. Because we are removing the rectangles, the area of the smaller rectangles will need to be subtracted from the total area of the triangle.



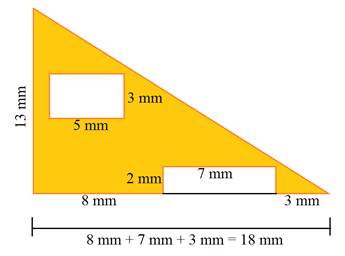
A _triangle = 1/2 bh                     A _{top rectangle} = bh      A _{bottom rectangle} = bh

A = 1/2 (18 mm)(13 mm)         A = (5 mm)(3 mm)    A = (7 mm)(2 mm)

A = 117 mm²                           A = 15 mm²              A = 14 mm²

Therefore, the total area of the orange figures is:

Let's Review

When asked to determine the area of an irregular figure, there are two main methods you can try. They both involve breaking the irregular figures into shapes that you can work with. Once you have done this you will need to either add the area of the pieces together or subtract the missing pieces from the whole.

Related Links: Math Geometry Area of a Square Area of Rectangle Area of Triangle