Right triangles are special. There is a formula, called the Pythagorean Theorem, that can be used to determine the length of the third side of a right triangle if you are given the length of the other two sides.



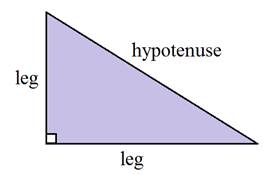
The two sides that meet at a right angle are called the legs. The side across from the right angle is the longest of the three and is called the hypotenuse.

This is important to remember when using the Pythagorean Theorem.

a² + b² = c²

Let's take a look at how the theorem works.

The a and b represent the lengths of the legs and the c represents the length of the hypotenuse.



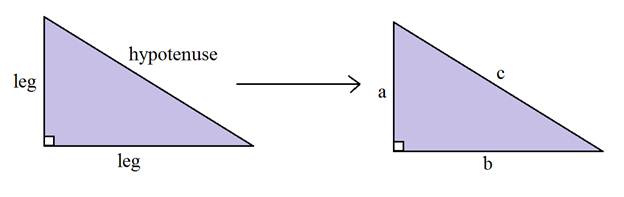
It is very important that the hypotenuse is labeled correctly. It is always across from the right angle and labeled as c. The other two are a and b and it doesn't matter which is a and which is b.

Now let's see the formula in action.



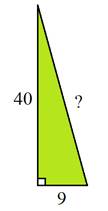
#1)

Step 1: Label the sides of the triangle. (Remember that side c is across from the right angle.)



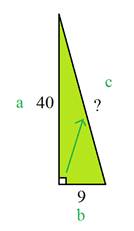
Step 2: Plug the numbers into the formula.

a² + b² = c²

40²+ 9² = c²

Step 3: Start to solve.

Follow the order of operations to solve for c.

40² + 9² = c²   Square each of these numbers.

1600 + 81 = c²    Next, add the squares of the legs.

1681 = c²   Now, take the square the square root of the sum.

√1681 = √c²   If you need to, use the square root button on the calculator.

41 = c

Therefore, the third side of the triangle is 41 units.



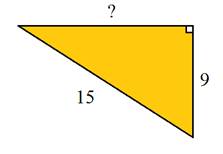
#2)

Step 1:Label the triangle.



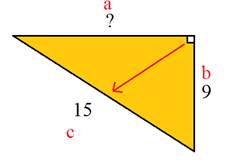
Step 2: Set up the equation.

a² + b² = c²

a² + 9² = 15²

Step 3:Solve the equation.

a²+ 81 = 225

Because we only have one leg in     a² = 225 - 81

we need to subtract the square of     a² = 144

the leg from the square of the     √a² = √144

hypotenuse.     a = 12

Therefore, the length of the missing side is 12 units.

#3)



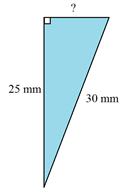
Step 1:Start by labeling the triangle.



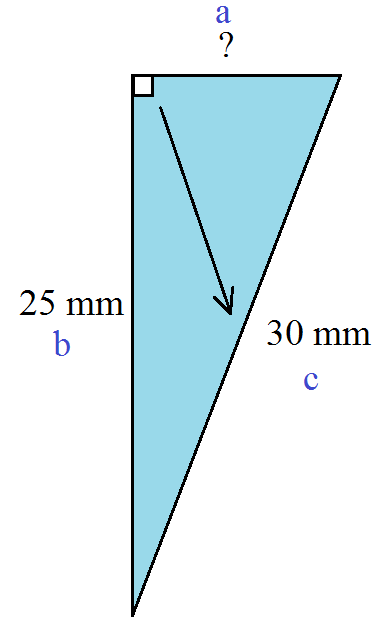
Step 2:Set up the formula

a² + b² = c²

a² + 25² = 30²

Step 3:Now start solving.

a² = 625 + 900

a² = 900 - 625

a² = 275

√a² = √275

a = 16.583123....

Notice that in this example, the answer is not a nice whole number.

Instead, it is irrational. That means that the number after the decimal point

never ends and never repeats. When this happens it is useful to round the answer.

The length of side a is approximately 16.6 mm.

Let's Review

The Pythagorean Theorem is a useful formula for determining the length of a side of a right triangle. The hypotenuse is the longest side of the triangle and should be labeled c. You can locate the longest side by looking across from the right angle. The legs are a and b. It does not matter which is which when labeling. Once you have them labeled, you can plug the values into the formula a² + b² = c² and solve for whichever one is missing. If the square root is not a whole number, when solving, check to see if the directions ask you to round the answer to a certain place value. It might be the nearest tenth or the nearest hundredth.

Related Links: Math Geometry Pythagorean Theorem Worksheets