You may already know that triangles have 180° and quadrilaterals have 360°. However, do you know how many degrees are in a pentagon or a dodecagon? Let's take a look at some of the polygons to find a pattern.



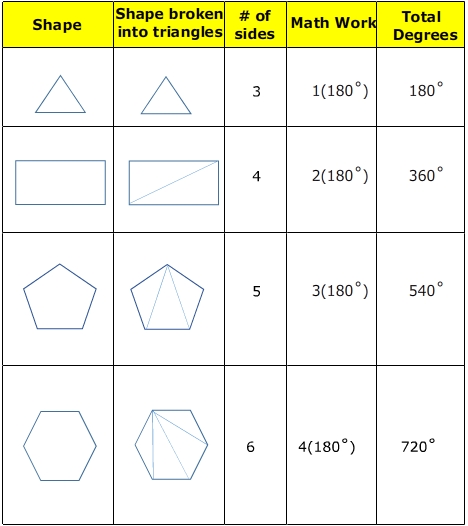
Notice that the number of triangles is 2 less than the number of sides in each example. The number of degrees inside the polygon can be determined by multiplying the number of triangles in the shape by 180 degrees. And the number of triangles is 2 less than the number of sides.



Let's use the formula in a few examples.

Example 1: How many degrees are in a nonagon?

Step 1: Determine the number of sides in a nonagon. Nonagons have 9 sides.

Step 2: Evaluate the formula for n = 9.

(n - 2)180°

(9 - 2)180°

7 x 180°

1260°

A nonagon has 1260°.

Example 2: How many degrees are in a dodecagon?

Step 1: Determine the number of sides in a dodecagon. Dodecagons have 12 sides.

Step 2: Evaluate the formula for n = 12.

(n - 2)180°

(12 - 2)180°

10 x 180°

1800°

A dodecagon has 1800°.

Example 3: How many degrees are in a 23-gon?

Although polygons do have official names, many mathematicians refer to some of the many sided figures by just using the number of sides followed by "gon."

Step 1: Using the name, determine how many sides the shape has.

This shape has 23 sides.

Step 2: Evaluate the formula for n = 23.

(n - 2) 180°

(23 - 2)180°

21 x 180°

3780°

A polygon with 23 sides has a total of 3780 degrees.

Let's Review

To determine the total sum of the interior angles, you need to multiply the number of triangles that form the shape by 180°. The number of triangles is always two less than the number of sides. This gives us the formula

total interior angles = (n - 2)180°, where n is the number of sides.

Related Links: Math Geometry Interior Angles of a Polygon Polygon Shapes