Do you remember the formula for the volume of a cylinder?
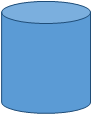
That's right, it was V = Πr²h.

But what happens when the cylinder is cut into three equal sized pieces?



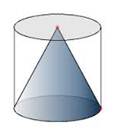
You get a cone! Yes, one of the pieces is a cone. Because all three pieces are equal, the volume of the cone formed is one-third of the total volume.

You might also notice that the cone has the same height as the cylinder and the same area of the base as the cylinder. Therefore, the volume of the cone would

be one third of the volume of the cylinder.   

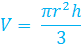
Let's see this formula in action!

Example 1: Determine the volume of the cone.

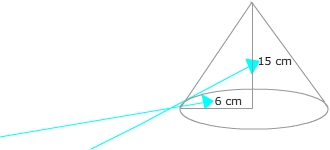
In this example, the radius is 6 cm and the height is 15 cm.

These values will be "plugged" into the formula and solved.





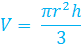
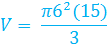
  "Double Duty" on this step. Both the 6 was squared and the 15 and 3 were divided.

  This is the exact answer, also referred to as "in terms of pi."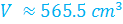

This is an approximation to the nearest tenth.

Example 2: Determine the volume of the cone.



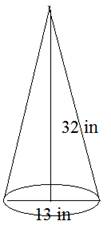
In this case, the diameter and the height are given. Be sure to divide the diameter in half to determine the radius of the base of the cone.   13 in ÷ 2 = 6.5 in

Now use the given information and the formula.











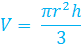
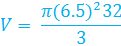
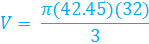
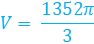
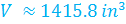
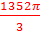You can stop at cubic inches for an exact answer, or you can round your answer. In this case, the answer was rounded to the nearest tenth to get 1415.8 cubic inches.

Don't be fooled by a cone on its side.



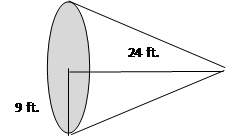
Be sure to locate the circular base. Look to the base to find either the radius or diameter of the cone. This cone gives the radius of 9 ft.

The other measurement of 24 ft. from the base to the tip is the height of the cone.

Now we are ready to determine the volume of the cone.











The volume of this cone is exactly 243Π cubic feet which is approximately 763.4 cubic feet.

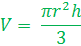
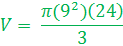
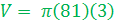
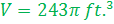
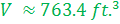
Let's Review

The process for determining the volume of a cone is very similar to determining the volume of a cylinder. A cone has one-third the volume of a cylinder with the same base. So we can determine the volume of the corresponding cylinder and divide by 3. That gives the volume formula as

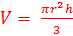
Once you begin to use the formula, you can either decide to keep the answer exact by leaving it in terms of pi or you can give an approximate answer by rounding the answer to a given place value.

Related Links: Math Geometry Volume of Cone