Calculating the volume of a cylinder is very similar to determining the area of a prism. You can think of a cylinder as being made up of many disks.



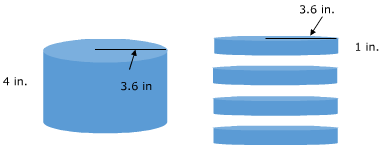
So if we find the area of one disk and multiply by the number of disks, we have the volume.

Recall that the area of a circle is equal to pi times the radius squared. And the number of disks can be thought of as the height. This gives us a volume formula.



Let's give the formula a try.

V = Πr²h

V = Π(3.6)²(4)        Here we started by replaced r with the radius and h with the height.

V = Π(12.96)(4)      Using the order of operations, the radius was squared first.

V = 51.84Π             Then we multiplied by 4. This is the answer in terms of pi.

V ≈ 162.86 in.³       After multiplying by Π, the answer was rounded to the nearest hundredth.

Here is another example:



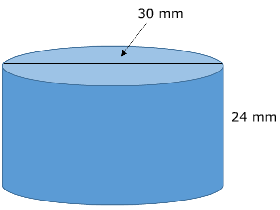
Notice that in this example, the diameter is given instead of the radius.

Divide the diameter in half to get the radius.      30 mm ÷ 2 = 15 mm

Next, plug the values into the formula and solve.

V = Πr²h

V = Π(15)²(24)

V = Π(225)(24)

V = 5400Π mm³   ← If you are looking for an exact answer, STOP here!

V ≈ 16,964.6 mm³   ← Otherwise, you can round your answer to get an approximate. This solution is rounded to the nearest tenth.

Don't be tricked by cylinders on their sides!



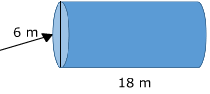
If it helps, try drawing a new sketch of the cylinder with the circular base on the bottom.



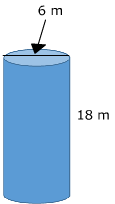
Now it may be clearer to see that the diameter of the base is 6 m and the height of the cylinder is 18 m. Use these measurements to calculate the volume. Be sure to first cut the diameter in half to determine the radius.

6m ÷ 2 = 3m Therefore, the radius is 3 meters.

V = Πr²h

V = Π(3)²(18)

V = Π(9)(18)

V = 162Π m³ ← Remember that this is the exact answer.

V ≈ 509 m³ ← This is an approximate answer, rounded to the nearest whole.

Let's Review

To calculate the volume of a cylinder, multiply the area of the base (Πr²) times the height (h). This gives the formula V = Πr²h. Because pi is an irrational number, you may need to round your answer. If an exact answer is needed, leave the pi in the solution. Other key things to notice when solving include determining whether you have the diameter or the radius and if the cylinder is upright or not. If you have the diameter, divide the length in half to determine the radius. If the cylinder is on its side, you could redraw the object the make sure that you have correctly labeled which length is the radius and which is the height. Then you are ready to solve!

Related Links: Math Geometry Volume of Cylinder