Component Form and Magnitude

A vector is a quantity with both magnitude and direction. To differentiate vectors from variables, constants and imaginary numbers vectors are denoted by a lowercase boldface variable, v, or a variable with a harpoon arrow above it,

\overset{⇀}{v}

.

In this discussion vectors will be denoted by lowercase boldface variables. Examples of vector quantities are velocity, acceleration and force.

Figure 1 shows two vectors v and u as directed line segments.

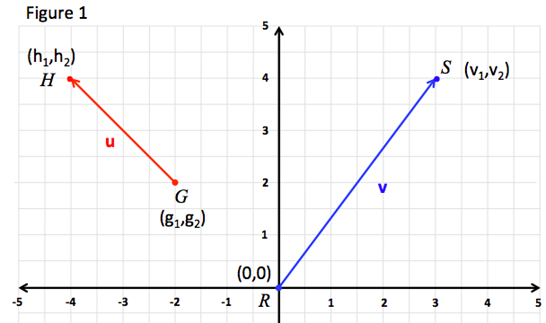
The vector v is represented by the directed line segment

\overset{⇀}{R S}

and has an initial point at R and a terminal point at S.

Vectors are often represented in component form. Vector v in Figure 1 has an initial point at the origin (0,0) and is said to be in standard position. A vector in standard position can be represented by the coordinates of its terminal point. Thus vin component form =

〈 v_{1}, v_{2} 〉

Notice that the brackets surrounding the vector components v₁ and v₂ are pointed not round like parentheses.

The magnitude of v or

\overset{⇀}{R S}

is represented by

∥ \overset{⇀}{R S} ∥

∥ v ∥

and is calculated using the Distance Formula,

∥ v = \sqrt{v_{1}^{2} + v_{2}^{2}} ∥

MAGNITUDE OF A VECTOR:

$∥ v = \sqrt{v_{1}^{2} + v_{2}^{2}} ∥$

Vector u represented by

\overset{⇀}{G H}

in Figure 1 is not in standard position as its initial point is not the origin (0,0). The component form and magnitude of vector u can be calculated as follows:

COMPONENT FORM OF DIRECTED LINE SEGMENT:

Initial point: G (g₁, g₂)
Terminal Point: H (h₁, h₂)

$\overset{⇀}{G H} = 〈 h_{1} - g_{1}, h_{2} - g_{2} 〉 = 〈 u_{1}, u_{2} 〉 = u$

MAGNITUDE OF DIRECTED LINE SEGMENT:

Initial point: G (g₁, g₂)
Terminal Point: H (h₁, h₂)

$\overset{⇀}{∥ G H ∥} = \sqrt{{(h_{1} - g_{1})}^{2} + {(h_{2} - g_{2})}^{2}} = \sqrt{u_{1}^{2} + u_{2}^{2}}$

Let's look at a couple examples.

Example 1: Find the component form and magnitude of vector u in Figure 1.

Step 1: Identify the initial and terminal coordinates of the vector.

Initial Point G: (-2, 2)

Terminal Point H: (-4, 4)

Step 2: Calculate the components of the vector.

Subtract the x-component of the terminal point from the x-component of the initial point for your x-component of the vector. Do the same for the y-components.

$u = 〈 h_{1} - g_{1}, h_{2} - g_{2} 〉 = 〈 u_{1}, u_{2} 〉$

$u = 〈 - 4 - (- 2), 4 - 2 〉$

$〈 - 2, 2 〉 = u$

Step 3: Calculate the magnitude of the vector.

||u|| = $\sqrt{u_{1}^{2} + u_{2}^{2}}$

||u|| = $\sqrt{{(- 2)}^{2} + {(2)}^{2}}$

$\sqrt{4 + 4}$

$\sqrt{8}$

Example 2: Find the component form and magnitude of vector v in standard position with terminal point (8, -2).

Step 1: Identify the initial and terminal coordinates of the vector.

Because vector v is in standard position it's initial point is (0,0)

Initial Point: (0, 0)

Terminal Point: (8, -2)

Step 2: Calculate the components of the vector.

Subtract the x-component of the terminal point from the x-component of the initial point for your x-component of the vector. Do the same for the y-components.

In this case the vector is in standard form therefore the components of the vector are the same as the components of the terminal point.

$v = 〈 v_{1} - 0, v_{2} - 0 〉 = 〈 v_{1}, v_{2} 〉$

$v = 〈 8 - 0, - 2 - 0 〉$

$〈 8, - 2 〉 = v$

Step 3: Calculate the magnitude of the vector.

||v|| = $\sqrt{v_{1}^{2} + v_{2}^{2}}$

||v|| = $\sqrt{{(8)}^{2} + {(- 2)}^{2}}$

$\sqrt{64 + 4}$

$\sqrt{68}$

$2 \sqrt{17}$

Related Links:
Math
algebra
Scalar Multiplication and Vector Addition
Unit Vectors
Pre Calculus

To link to this Component Form and Magnitude page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/component_form_and_magnitude/">Component Form and Magnitude</a>

Component Form and Magnitude

More Topics

Educational Videos