Polar Coordinates: Coordinate Conversion

A polar coordinate system in a plane contains a fixed point, called a pole or origin from which a ray is drawn horizontally, called the polar axis. The polar axis corresponds to the positive x-axis in the Cartesian coordinate system.

Let T be any point in the plane with a distance r from the origin 0 and the angle θ the distance between the polar axis and line

\bar{T O}

. Point T has polar coordinates (r, θ) with θ usually measured in radians.

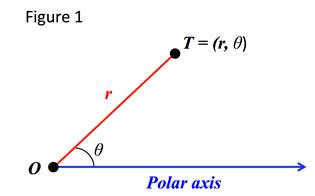
The angle θ is considered to be positive if measured in the counterclockwise direction from the polar axis and negative if measured clockwise. The pole or origin has polar coordinates (0, θ).

One important difference between Cartesian coordinates and polar coordinates is that in the Cartesian coordinate system each point has a unique set of coordinates. In the polar coordinate system for example (r, θ) and (r,θ + 2π) represent the same point as do (r, θ) and (-r,θ + π).

In general terms and point (r, θ) can also be written as (r,θ + 2nπ) or (-r,θ + (2n + 1) π), where n is any integer.

POLAR COORDINATES:

In the polar coordinate system point (r, θ) can also be written as:

$(r, θ + 2 n π)$ or $(- r, θ + (2 n + 1) π)$

where n is any integer.

To convert between polar coordinates and Cartesian coordinates, also called rectangular coordinates, the following relationships are used:

COORDINATE CONVERSION RELATIONSHIPS:

$x = r \cos θ$ $\tan θ = y / x$

$y = r \sin θ$ $r^{2} = x^{2} + y^{2}$

Let's use these coordinate conversion relationships in some examples:

Example 1: Convert each point from polar coordinates to rectangular coordinates. a)

(3, π)

(5, \frac{π}{6})

(- 6, \frac{π}{4})

Step 1: Determine the rectangular coordinates for $(3, π)$ .

$(3, π)$ : r = 3, θ = π

$x = r \cos θ = 3 \cos π = - 3$

$y = r \sin θ = 3 \sin π = 0$

$(3, π) \to (- 3, 0)$

Step 2: Determine the rectangular coordinates for $(5, \frac{π}{6})$ .

$(5, \frac{π}{6})$ : $r = 5, θ = \frac{π}{6}$

$x = r \cos θ = 5 \cos \frac{π}{6} = 5 \cdot \frac{\sqrt{3}}{2} = \frac{5 \sqrt{3}}{2}$

$y = r \sin θ = 5 \sin \frac{π}{6} = 5 \cdot \frac{1}{2} = 2.5$

$(5, \frac{π}{6}) \to (\frac{5 \sqrt{3}}{2}, 2.5)$

Step 3: Determine the rectangular coordinates for $(- 6, \frac{π}{4})$ .

$(- 6, \frac{π}{4})$ : $r = - 6, θ = \frac{π}{4}$

$x = r \cos θ = - 6 \cos \frac{π}{4} = - 6 \cdot \frac{\sqrt{2}}{2} = - 3 \sqrt{2}$

$y = r \sin θ = - 6 \sin \frac{π}{4} = - 6 \cdot \frac{\sqrt{2}}{2} = - 3 \sqrt{2}$

$(- 6, \frac{π}{4}) \to (- 3 \sqrt{2}, - 3 \sqrt{2})$

Example 2: Convert the following rectangular coordinates to polar coordinates. a) (0, 3) b) (1, 1) c)

(5, 5 \sqrt{3})

Step 1: Determine the polar coordinates for (0, 3).

Note that the answer is just one set of polar coordinates. There are other equivalent polar coordinates.

$(0, 3) : x = 0, y = 3$

$r^{2} = x^{2} + y^{2} = 0^{2} + 3^{2} = 9$

$r = \pm \sqrt{9} = \pm 3$

$\tan θ = \frac{y}{x} = \frac{3}{0} \to u n d e f i n e d$

However since (0, 3) falls on the y-axis we know that $θ = 90 ° = \frac{π}{2}$ and the value of r should be positive.

$(3, 0) \to (3, \frac{π}{2})$

Step 2: Determine the polar coordinates for (1, 1).

Note that the answer is just one set of polar coordinates. There are other equivalent polar coordinates.

$(1, 1) : x = 1, y = 1$

$r^{2} = x^{2} + y^{2} = 1^{2} + 1^{2} = 2$

$r = \pm \sqrt{2}$

$\tan θ = \frac{y}{x} = \frac{1}{1} = 1$

$θ = \tan^{- 1} 1 = \frac{π}{4}$

Since (1, 1) falls in quadrant 1 and $\frac{π}{4}$ falls in quadrant 1 then the value of r is positive.

$(3, 0) \to (3, \frac{π}{2})$

Step 3: Determine the polar coordinates for $(5, 5 \sqrt{3})$

Note that the answer is just one set of polar coordinates. There are other equivalent polar coordinates.

$(5, 5 \sqrt{3}) : x = 5, y = 5 \sqrt{3}$

$r^{2} = x^{2} + y^{2} = 5^{2} + {(5 \sqrt{3})}^{2} = 100$

$r = \pm \sqrt{100} = \pm 10$

$\tan θ = \frac{y}{x} = \frac{5 \sqrt{3}}{5} = \sqrt{3}$

$θ = \tan^{- 1} \sqrt{3} = \frac{π}{3}$

Since $(5, 5 \sqrt{3})$ falls in quadrant 1 and $\frac{π}{3}$ falls in quadrant 1 then the value of r is positive.

$(5, 5 \sqrt{3}) \to (10, \frac{π}{3})$

To link to this Polar Coordinates: Coordinate Conversion page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/polar_coordinates_coordinate_conversion/">Polar Coordinates: Coordinate Conversion</a>

Polar Coordinates: Coordinate Conversion

More Topics

Educational Videos