Properties of Real Numbers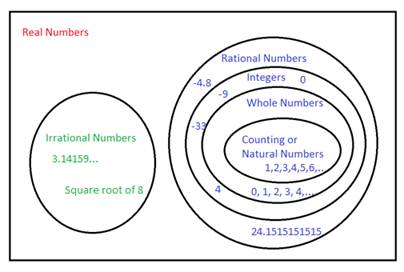 Remember that the real numbers are made up of all the rational and irrational numbers. The properties help us to add, subtract, multiply, divide, and various other mathematical operations. Here is a brief look at several of the properties: Commutative: a + b = b + a & ab = ba This property is all about the order. If you switch the order of the numbers when adding or multiplying, the answer doesn't chance. Examples: 3 x 4 = 4 x 3 and 3 + 4 = 4 + 3 12 = 12 7 = 7 Associative: a(bc) = (ab)c & a + (b + c) = (a + b) + c This property is all about the groups. Notice that the location of the parentheses can be changed and the answer is still the same. Examples: (5 + 6) + 3 = 5 + (6 + 3) and (3 x 2) x 4 = 3 x (2 x 4) 11 + 3 = 5 + 9 6 x 4 = 3 x 8 14 = 14 24 = 24 Distributive: a(b + c) = ab +ac This property is all about dealing with a number outside the parentheses when there is a sum or difference inside. Check out how the number outside can be used. Examples: 4(3 + 5) = 4(3) + 4(5) or 4(8 - 7) = 4(8) - 4(7) 4(8) = 12 + 20 4(1) = 32 - 28 32 = 32 4 = 4 Multiplication Property of Zero: m*0 = 0 Ever noticed this handy little property? Any time you multiply something by zero, you get zero. It doesn't matter what the real number is, if you multiply by zero, you get zero! Examples: 4 x 0 = 0, 15 x 0 = 0, 1 1/2 x 0 = 0, -32 x 0 = 0 Identity Property: a + 0 = a & a * 1 = a For addition, this property says that you can add 0 and not change the value of the number. So 4 + 0 = 4 or -13 + 0 = -13. The additive identity is 0! For multiplication, this property says that you can multiply by 1 and not change the value of the number. So 4 x 1 = 4 and -13 x 1 = -13. The multiplicative identity is 1! Inverse: a + (-a) = 0 and a *  = 1 = 1The inverse property is all about undoing. To "undo" you could add the additive inverse. In other words, when you add a number and its opposite or additive inverse you get 0. Examples: 4 + (-4) = 0 or -5.8 + 5.8 = 0 You could also multiply by the reciprocal or multiplicative inverse to get 1. Examples: 8 x 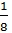 = 1 or -15 x = 1 or -15 x 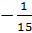 = 1 = 1*Note that dividing by 0 is undefined. 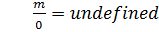 Closure This property is all about the answers you get. If you do something to two real numbers and always get a real number answer, you could say that real numbers are closed under that operation. For example: If you add any two real numbers, you will get a real number sum. Therefore, real numbers are closed under addition. In addition, if you multiply any two real numbers, you will get a real number product. Therefore, real numbers are closed under multiplication. Using these properties will help you carry out and simplify lots of other operations or more complex math problems! Use them to help you learn your math facts even faster as well.
To link to this Properties of Real Numbers page, copy the following code to your site: |
More TopicsEducational Videos |
