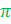There are several "famous" and helpful irrational numbers. You might be the most familiar with the number pi, or , but there is also the number e.

e = 2.7182818284590452353602874713527...
The number e is called Euler's Number because it was first used by Leonhard Euler in the 1700s. (Many mathematicians pronounce Leonhard Euler's name as "Oiler" instead of "Yuler"). However, another mathematician named John Napier used the number back in the 1600s with logarithms. Napier just didn't call it e yet.

It is equal to the base of the natural logarithm.

ln x = log_e^x

Euler's number is irrational, which means that the decimal never terminates, or ends, and it does not repeat. The digits after the decimal continue indefinitely. That means that it is impossible to write an exact value to represent e, but there are some expressions that are approximate values of e.

One possible way to approximate the value of e is using an infinite series:





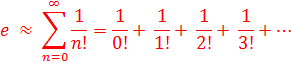
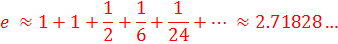
Another way to approximate e is to use the expression 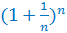As the value of n increases, the expression becomes closer and closer to the value of .

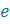The number 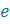, becomes helpful in many different mathematical situations, like determining the compounded interest on continuously compounded bank accounts. In fact, this very use of the value of e is how Euler came up with the number.



We can use this formula to determine the amount in the account when we know the principal amount, the rate and the length of time the money will be in the account when compounded continuously.

Example:

Saraaj will deposit $1800 in an account at a rate of 3% that is compounded continuously. How much money will be in the account after 5 years?



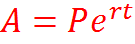
A = 1800e^(0.03)(5)

A = 1800e^0.15

A = 2091.3016...

A = $2091.30

Here, Euler's number was used to help determine that there would be approximately $2091.30 in the account after 5 years.

Once you get deeper into your math journey, you will find the e turns up everywhere! Euler's number is especially helpful in engineering, probability and trigonometry applications. For example, it is used in Newton's heating and cooling, it is used to relate trigonometric functions to hyperbolic functions, it is used in probability to represent the normal distribution and it is even used in calculations with electric circuits!


Related Links:
Math
algebra