Inverse Properties of Addition and Multiplication
Inverse Property of Addition says that any number added to its opposite will equal zero. What is the opposite you might ask? All you have to do is change the sign from positive to negative or negative to positive.
Let's see what that looks like.
Sometimes this can be written in a vertical format.
Inverse Property of Multiplication says that any number multiplied by its reciprocal is equal to one.
Let's start by defining a reciprocal. To find the reciprocal of any number write it as a fraction and then flip it.
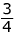 . Flip it →
. Flip it →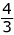 .
. 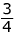 . is
. is 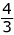 .
.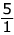 →flip it
→flip it 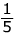
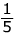
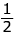 . → flip it
. → flip it 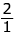
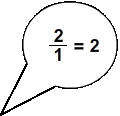
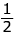 is 2
is 2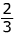 . → flip it -
. → flip it - 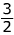

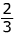 is -
is - 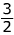
Special Reminder: To multiply fractions you multiply the numerator times the numerator and then the denominator times the denominator and then simplify your answer:
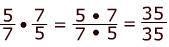 = 1
= 1Now let's look at how we can use this with the inverse of multiplication.
 (reciprocal) = 1
(reciprocal) = 1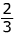

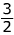 = 1 →
= 1 → 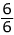 = 1
= 1

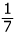 = 1 →
= 1 → 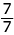 = 1
= 1Now let's summarize what we have learned.
The Inverse Property of Addition says that any number added to its opposite is equal to zero.
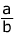

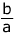 = 1
= 1Related Links:
Math
algebra
Trichotomy Property
Distributive Property
To link to this Inverse Properties of Addition and Multiplication page, copy the following code to your site:
