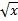Some common inverse functions would be the inverse of addition is subtraction, the inverse of x² would be and etc. The inverse trig functions are the inverse functions of sine, cosine, tangent, cotangent, secant and cosecant functions with suitably restricted domains. The purpose of the inverse functions is to determine the measure of an angle in a right triangle when given at least 2 side lengths

The inverse functions have the same name as the function but have the prefix "arc". Therefore, the inverse of sine is arcsine, cosine is arccosine, tangent is arctangent. Secant, cosecant and cotangent have inverses as well, but are less widely used. Most calculators have buttons for sine inverse, cosine inverse and tangent inverse.

The confusing part can be the notation for the inverse functions. On most calculators arcsine is denoted by sin^-1, arccosine is cos^-1 and arctangent is tan^-1. The negative one is not to be confused with the exponent -1.

Example: How to find the missing angle in a right triangle.



It does not matter which two sides of the triangle (trig ratio) is used to find the measure of angle A. An equivalent answer will be reached regardless. Refer to the example below.

                

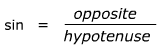
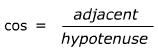
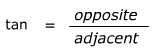
m∠A = 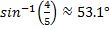     or     m∠A =  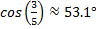    or     m∠A =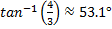

Angle B may be calculated by using an inverse trig function as well, however, the simplest method would be to subtract the measure of angle A from 90°. Recall that in a right triangle m∠A + m∠B = 90°. Therefore, m∠B = 90° - m∠A. Using the example above m∠B = 90°-53.1° = 36.9°.

Inverse trigonometric inverses are used frequently in engineering, navigation, architecture, aeronautics and physics. Whenever a right triangle can be determined you can use trigonometric functions and inverses to find side and angle measures.

Related Links: Math Trigonometry Quadrantal Angles Reference Angles