Angular Measurement
In a previous section, quantities that could be used to describe straight-line motion were introduced. These quantities were displacement, velocity, and acceleration. Rotational motion can be described using similar quantities.
In circular motion, an object rotates around a
fixed axis. This fixed axis is at rest, relative to the surroundings of the object. Every part of the object rotates around this fixed axis. We make the assumption that no part of the object bends or twists, so every part of the object moves in the same way relative to the other parts. This means that we assume that the object is
rigid.
In the frame of reference of the rotating object, the fixed axis passes through a point we label the origin, O. The plane of the object that is perpendicular to the axis at the point O is the xy plane. If we choose a point P somewhere within the rotating object, at a particular moment in time it will have a certain (x, y) coordinate. Keeping track of the changes in the (x, y) coordinates with time is complicated. This can be simplified by choosing the angle between the line OP and the +x axis to be the quantity of interest. This angle can be labeled θ, and we will use this as the
angular coordinate. The most effective way to measure the angle θ is in units of radians.
An arc of length s around the outside edge of a circle of radius r can be related to the angular coordinate using the formula,
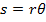
Both s and r have units of length, so in SI units, they are measured in meters. This shows that a radian is actually a ratio of two lengths. For this to be true, a radian must be a dimensionless quantity. It is merely a helpful "stand-in", or placeholder unit.
Angular Velocity
The rotational motion of an object can be described as the rate of change of the angular coordinate, θ. This rate of change of θ with respect to time is similar to the way displacement changes with time in linear motion. The rate of change of displacement in linear motion is called velocity. To make it clear that we are discussing a different quantity, we will call the rate of change of the angular coordinate with respect to time the
angular velocity. The SI unit of angular velocity is
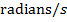
. This can also be written as
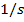
, or
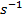
, because the radian is merely a "stand-in" unit. The symbol for angular velocity is the Greek letter
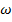
(lower-case "omega").
If an object rotating in the xy plane makes an angle of θ
1 with respect to the +x axis at time t
1, and later makes an angle of θ
2 with respect to the +x axis at time t
2, then the change in the angular coordinate can be written,
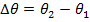
The change in time can be written,
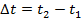
These formulas use the Greek letter

(upper-case "delta") to mean "the change in".
If the object is rotating in the xy plane, then we can write the angular velocity as a rotation around the z axis,
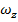
. The angular velocity is,
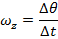
The rate of change of
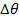
divided by
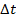
does not have to be constant. The angular velocity of the object at any particular time is called the instantaneous angular velocity. However, between any two times, the "average" angular velocity can be found. For
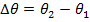
and
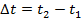
, the average angular velocity is,
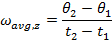
This description assumed that the rotation axis was always along the z axis. Angular velocity is a vector, and so it is possible for the axis of rotation to point in any direction. Expressed as a vector, the angular velocity is written
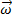
, and it has x, y, and z axes. What is important is that the angular velocity vector points in the direction of the axis of rotation, not the direction of motion, as the velocity vector does in linear motion.
Angular Acceleration
A change in the angular velocity with respect to time is called the angular acceleration. Angular acceleration is the rate of change of an object's angular velocity. The SI unit of angular acceleration is
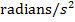
. This can also be written as
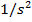
, or
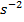
, because the radian is merely a "stand-in" unit. The symbol for angular acceleration is the Greek letter
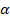
(lower-case "alpha").
If an object rotating in the xy plane (and therefore rotating around the z axis) has an angular velocity
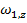
at time t
1, and later has an angular velocity
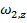
at time t
2, then the change in the angular velocity can be written,
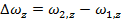
The change in time can be written,
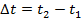
These formulas use the Greek letter

(upper-case "delta") to mean "the change in".
Since the object is rotating in the xy plane, then we can write the angular acceleration as a rotation around the z axis,
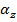
. The angular acceleration is,
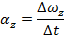
The rate of change of
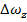
divided by
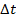
does not have to be constant. The angular acceleration of the object at any particular time is called the instantaneous angular acceleration. However, between any two times, the "average" angular acceleration can be found. For
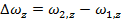
and
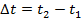
, the average angular acceleration is,
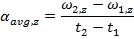
This description assumed that the rotation axis was always along the z axis. Angular acceleration is a vector, and so it is possible for the axis of rotation to point in any direction. Expressed as a vector, the angular acceleration is written
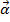
, and it has x, y, and z axes. What is important is that the angular acceleration vector points in the direction of the
axis of rotation, not the direction of motion, as the acceleration vector does in linear motion.
In AP Physics, changes in angular acceleration with respect to time are generally not considered, so the average angular acceleration will typically be equivalent to the instantaneous angular acceleration.
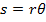
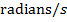 . This can also be written as
. This can also be written as 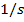 , or
, or 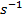 , because the radian is merely a "stand-in" unit. The symbol for angular velocity is the Greek letter
, because the radian is merely a "stand-in" unit. The symbol for angular velocity is the Greek letter 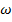 (lower-case "omega").
(lower-case "omega").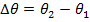
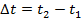
 (upper-case "delta") to mean "the change in".
(upper-case "delta") to mean "the change in".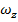 . The angular velocity is,
. The angular velocity is,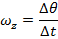
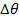 divided by
divided by 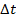 does not have to be constant. The angular velocity of the object at any particular time is called the instantaneous angular velocity. However, between any two times, the "average" angular velocity can be found. For
does not have to be constant. The angular velocity of the object at any particular time is called the instantaneous angular velocity. However, between any two times, the "average" angular velocity can be found. For 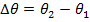 and
and 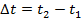 , the average angular velocity is,
, the average angular velocity is,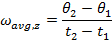
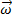 , and it has x, y, and z axes. What is important is that the angular velocity vector points in the direction of the axis of rotation, not the direction of motion, as the velocity vector does in linear motion.
, and it has x, y, and z axes. What is important is that the angular velocity vector points in the direction of the axis of rotation, not the direction of motion, as the velocity vector does in linear motion.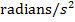 . This can also be written as
. This can also be written as 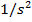 , or
, or 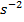 , because the radian is merely a "stand-in" unit. The symbol for angular acceleration is the Greek letter
, because the radian is merely a "stand-in" unit. The symbol for angular acceleration is the Greek letter 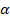 (lower-case "alpha").
(lower-case "alpha").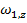 at time t1, and later has an angular velocity
at time t1, and later has an angular velocity 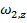 at time t2, then the change in the angular velocity can be written,
at time t2, then the change in the angular velocity can be written,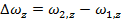
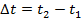
 (upper-case "delta") to mean "the change in".
(upper-case "delta") to mean "the change in".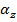 . The angular acceleration is,
. The angular acceleration is,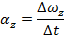
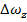 divided by
divided by 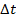 does not have to be constant. The angular acceleration of the object at any particular time is called the instantaneous angular acceleration. However, between any two times, the "average" angular acceleration can be found. For
does not have to be constant. The angular acceleration of the object at any particular time is called the instantaneous angular acceleration. However, between any two times, the "average" angular acceleration can be found. For 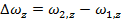 and
and 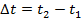 , the average angular acceleration is,
, the average angular acceleration is,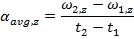
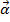 , and it has x, y, and z axes. What is important is that the angular acceleration vector points in the direction of the axis of rotation, not the direction of motion, as the acceleration vector does in linear motion.
, and it has x, y, and z axes. What is important is that the angular acceleration vector points in the direction of the axis of rotation, not the direction of motion, as the acceleration vector does in linear motion.