Uniform Circular Motion
For an object to move along a curved path, the direction of its velocity must change. A change in velocity means that there must be an acceleration that is not in the same direction as the velocity. For an object to move along a circular path, this means that there must be an acceleration that is always perpendicular to the velocity. This acceleration vector is therefore always directed toward the center of a circle formed by the object's path. This acceleration is either called the "radial acceleration", because it is at a certain radius from a central point, or the "centripetal acceleration", which means that it is "center seeking".
Uniform circular motion means that the magnitude of the velocity is a constant, and the direction of the velocity changes at a constant rate. This means that the object's path forms a circle, and that the object will complete repeated trips around the path in the same amount of time each time. If the radius of the circular path is R, and the magnitude of the velocity of the object is v, then the radial (centripetal) acceleration of the object is
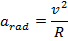
Again, this radial acceleration
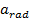
is always perpendicular to the direction of the velocity. The SI unit of this acceleration is
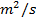
.
The radial acceleration can also be expressed in terms of the period of the motion T. The period T is the amount of time required to complete a revolution, or one trip around the circle, and is written in units of seconds s. If the magnitude of the velocity of an object traveling in uniform circular motion is v, and a velocity is a distance traveled in a certain time, then the velocity will be equal to the circumference (C) of the circle divided by the period,
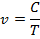
The circumference of the circle is equal to 2π multiplied by the radius R,
C = 2πR
At any point in the motion, the magnitude of the velocity is therefore
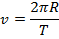
If this equation for v is substituted in to the equation for radial acceleration, the formula becomes
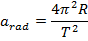 Non-Uniform Circular Motion
Non-Uniform Circular Motion
Non-uniform circular motion means that there is another acceleration that changes the magnitude of the velocity of the object. One example of non-uniform circular motion with would be a roller coaster car going around a vertical loop. At all points in the loop, the car experiences an inward radial acceleration, though the car also experiences acceleration due to gravity.
The radial acceleration is always perpendicular to the velocity vector of the object, though in non-uniform circular motion there is also an acceleration component that is parallel to the velocity vector. This is the "tangential acceleration", since this vector is always a tangent to the curve of the circular path. At any point on the circle, the total acceleration vector
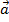
can be found by adding the radial and tangential accelerations using vector addition,
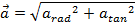
The magnitude of the object's velocity changes as it moves around the circle, though it is still possible to relate the velocity at any particular point to the radial acceleration. At any given position, the equation for the radial acceleration in terms of velocity is
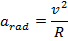 Dynamics of Circular Motion
Dynamics of Circular Motion
Newton's second law states that the sum of forces (also called the net force) on an object
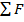
is equal to the mass multiplied by the acceleration of an object,
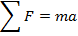
An object that is in circular motion has an acceleration that is always pointing toward the center of the circle. This means that the net force acting on the object is also a constant, inward-pointing force related to the centripetal acceleration.
For an object in uniform circular motion, the only acceleration is the inward-pointing radial (centripetal) acceleration,
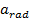
. The radial acceleration can be related to the velocity and the radius of the circular path,
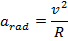
If the object has a mass m, then the net force acting on an object in uniform circular motion is
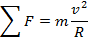
The radial acceleration can be also be related to the period of the object's motion around the circular path,
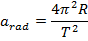
So, another way to express the net force acting on the object in uniform circular motion is
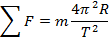 Circular Motion Free-Body Diagrams
Circular Motion Free-Body Diagrams
Drawing free-body diagrams can be very helpful when solving physics problems that involve circular motion. A free-body diagram shows all of the forces on the object that contribute to the net force.
Circular motion free body diagrams can be shown in different ways. One way is to show a view of the rotation from a viewpoint above (or below) the circular path. The inward-directed force can be shown with the object at any point along its path. It is important to note that the right-hand side of the sum-of-forces equation,
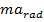
, does not appear in the free-body diagram. The radial acceleration may be shown in the diagram as a separate vector, as in the following free-body diagram.
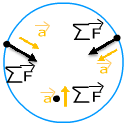
Another way to represent the free-body diagram is from the perspective of the object. This is very useful when considering things like the weight and normal forces acting on an object. For example, imagine being in a car going around a curve at a constant speed. The weight of the car is a downward force, and the normal force of the road is an upward force acting on the car. On the horizontal axis, a friction force acts on the tires, pushing them toward the center of the curve. The overall acceleration of the car is the radial acceleration directed inward. This scenario is shown in the following free-body diagram, showing the forces acting on the car as it turns to the right.

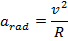
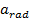 is always perpendicular to the direction of the velocity. The SI unit of this acceleration is
is always perpendicular to the direction of the velocity. The SI unit of this acceleration is 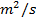 .
.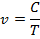
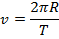
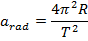
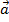 can be found by adding the radial and tangential accelerations using vector addition,
can be found by adding the radial and tangential accelerations using vector addition,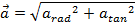
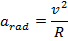
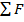 is equal to the mass multiplied by the acceleration of an object,
is equal to the mass multiplied by the acceleration of an object,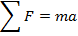
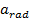 . The radial acceleration can be related to the velocity and the radius of the circular path,
. The radial acceleration can be related to the velocity and the radius of the circular path,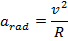
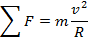
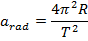
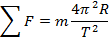
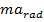 , does not appear in the free-body diagram. The radial acceleration may be shown in the diagram as a separate vector, as in the following free-body diagram.
, does not appear in the free-body diagram. The radial acceleration may be shown in the diagram as a separate vector, as in the following free-body diagram.
