Work and Potential Energy
Work (W) is the result of a force that acts on an object, causing the object to move from one place to another. The work-energy theorem (presented in the previous section) shows that the concepts of work and energy are equivalent. At the final position, the object will have a certain amount of kinetic energy (K). At the initial position, the object has "potential energy", which is energy associated with a certain position. Potential energy is assigned the letter U. The unit of potential energy is the same as the unit for work and kinetic energy, the Joule (J).
Potential Energy of Gravity
One situation in which there is a potential for work to be done is when an object is elevated a certain distance above the Earth. An object above the Earth is acted on by the force of gravity,
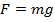
If an object is held at a displacement y above the surface of the Earth, and the surface of the Earth is taken to be the origin of coordinates (position zero), then the work done by the force of gravity as it acts on the object is,
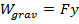
If the total work available in the system is
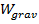
, then before the object falls, this must be equal to the potential energy of the system, U. The gravitational potential energy is therefore the product of the force of gravity and the height y above the origin,
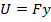
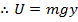
If an object falls from one height y
1 to a lower height y
2 (for example, if an object falls from the ceiling on to a table), then the initial gravitational potential energy is
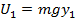
, and the final gravitational potential energy is
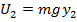
. The change in the potential energy U is the final value minus the initial value,
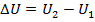
In this formula, the Greek uppercase letter

("delta") is used to mean "the change in".
The work done by gravity, as the object moves from height y
1 to lower height y
2 is,
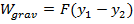
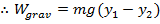
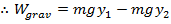
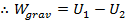
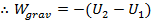
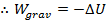
The work done by gravity is the negative of the change in potential energy. Therefore, as the object falls, potential energy is lost.
Conservation of Energy (Falling Object)
In a previous section, we saw that the total work is equal to the change in kinetic energy,
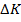
. In this case, the only force that acts on the object is the force due to gravity, so the total energy is equal to
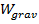
, and
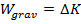
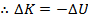
This shows how, as the object falls, the potential energy of the system is converted into the kinetic energy of the object. The idea that energy changes form leads to the idea of conservation of energy.
If the initial kinetic energy is K
1, the final kinetic energy is K
2, the initial potential energy is U
1, and the final potential energy is U
2, then,
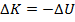
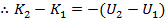
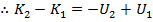
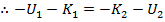
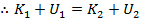
Therefore, the sum of the kinetic and potential energies at the starting position is equal to the sum of the kinetic and potential energies at the final position. This means that the total energy is the same at both positions. This total energy can be represented by E,
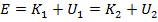
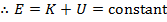
(if gravity is the only force doing work)
In this situation, in which gravity is the only force that is doing work, the energy changes form, but the total energy is a constant value. This is called conservation of energy, and it is a very important concept in physics. It is also important to note, though, that it is true only when all of the forces are known. A change to the formula is needed when the system is able to gain or lose energy. This is known as energy non-conservation.
Non-Conservation of Energy (Falling Object)
If gravity is not the only force acting on a falling object, then the previous equations for the work due to gravity
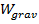
are still true, but the total work
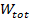
is,
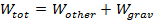
In this equation,
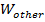
is the work done by all other forces, and
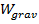
is the work done by gravity. The change in kinetic energy is always equal to the total work,
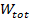
, and so,
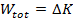
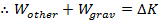
The work done by gravity is equal to
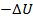
, and so the equation becomes,
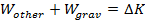
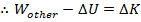
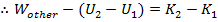
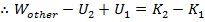
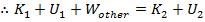
(if forces other than gravity do work)
An example of a force besides gravity that can do work is air resistance.
The equations for kinetic and potential energy for falling objects can be used to create another equation, that relates the positions and velocities of the object as it moves through its path,

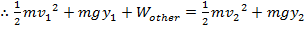
(if forces other than gravity do work)
Elastic Potential Energy
Potential energy applies to many other situations. One example was discussed in a previous section, and has to do with the work required to stretch or compress an elastic object, like a spring. When a spring is compressed, there is energy "stored". The energy is stored in the elastic deformation of the spring. This is called elastic potential energy.
Picture an object attached to a spring. If the magnitude of the displacement of the object labeled x, and so the equilibrium position is x = 0, then the force exerted on the object at displacement x is,
F = kx
The constant k in this equation is the spring constant, which is different for every spring. The spring constant has units Newtons per meter,
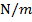
. The work that must be done on the spring to move the object from any starting position x
1 to a final position x
2 is,
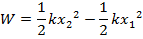
This equation was presented in a previous section. It is important to note that this equation is the work that must be done on the spring. This means it is an external force that is acting on the system. If the spring is released, then there is work that can be done by the spring. This elastic work can be labeled
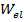
, and is,
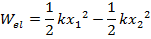
Note that the displacement values x
1 and x
2 are in the opposite order to the previous equation.
The elastic potential energy can be defined using this equation for work done by the spring. The elastic potential energy is,
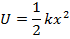
The spring constant k has units Newtons per meter,
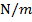
, and the potential energy unit is the Joule (J).
The elastic work can be related to the elastic potential energy at the displacement values x
1 and x
2,
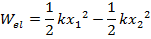
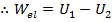
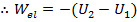
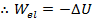 Conservation of Energy (Elastic)
Conservation of Energy (Elastic)
The total work is equal to the change in kinetic energy,
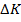
. In this case, the only force that acts on the object is the force of the spring, so the total energy is equal to
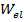
, and
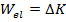
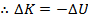
If the kinetic energy at displacement x
1 is K
1, the kinetic energy at x
2 is K
2, the potential energy at x
1 is U
1, and the potential energy at x
2 is U
2, then,
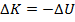
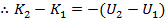
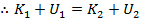
This means that the total energy is the same at both displacements. This total energy can be represented by E,
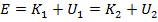
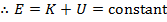
(if the elastic force is the only force doing work)
As with gravity, if all of the forces are known, the energy may change form, but the total energy is conserved.
Non-Conservation of Energy (Elastic)
If the force of the spring is not the only force that acts on the object, the total work
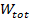
is,
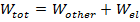
In this equation,
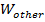
is the work done by all other forces, and
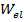
is the work done by the spring. The change in kinetic energy is always equal to the total work,
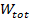
, and so,
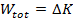
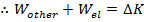
Since
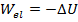
, the equation becomes,
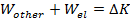
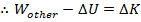
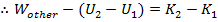
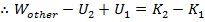
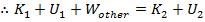
(if the elastic force is not the only force doing work)
For springs, sometimes energy is lost to heating the metal or permanent deformations. These are some examples that could be described by a
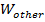
value.
An equation for springs relating displacements and velocities is,

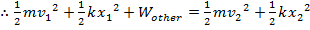
(if forces other than elastic do work)
Energy Conservation and Non-Conservation
The fact that the same equations relating kinetic and potential energy appeared for both gravitational and elastic forces is not a coincidence. In general, any system in which work is done can be described by one of the equations. Either it is a situation with energy conservation, or a situation with energy non-conservation. Energy conservation is described by the equation,
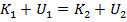
(energy conservation)
An important feature of situations in which energy is conserved is that it is possible to convert back and forth between kinetic and potential energy. The situation is called
reversible.
Energy non-conservation is described by the equation,

(energy non-conservation)
In a situation with energy non-conservation, energy can be converted between kinetic and potential energy, but the system gains or loses energy in the process. The situation is called
irreversible.
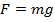
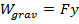
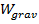 , then before the object falls, this must be equal to the potential energy of the system, U. The gravitational potential energy is therefore the product of the force of gravity and the height y above the origin,
, then before the object falls, this must be equal to the potential energy of the system, U. The gravitational potential energy is therefore the product of the force of gravity and the height y above the origin,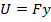
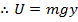
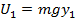 , and the final gravitational potential energy is
, and the final gravitational potential energy is 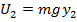 . The change in the potential energy U is the final value minus the initial value,
. The change in the potential energy U is the final value minus the initial value,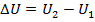
 ("delta") is used to mean "the change in".
("delta") is used to mean "the change in".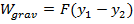
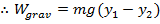
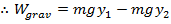
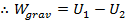
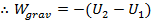
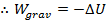
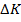 . In this case, the only force that acts on the object is the force due to gravity, so the total energy is equal to
. In this case, the only force that acts on the object is the force due to gravity, so the total energy is equal to 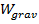 , and
, and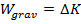
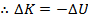
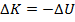
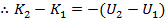
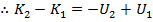
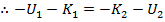
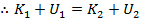
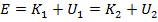
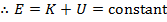 (if gravity is the only force doing work)
(if gravity is the only force doing work)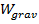 are still true, but the total work
are still true, but the total work 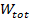 is,
is,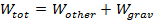
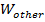 is the work done by all other forces, and
is the work done by all other forces, and 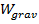 is the work done by gravity. The change in kinetic energy is always equal to the total work,
is the work done by gravity. The change in kinetic energy is always equal to the total work, 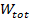 , and so,
, and so,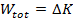
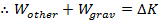
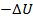 , and so the equation becomes,
, and so the equation becomes,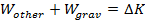
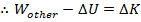
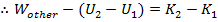
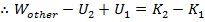
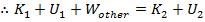 (if forces other than gravity do work)
(if forces other than gravity do work)
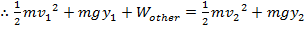 (if forces other than gravity do work)
(if forces other than gravity do work)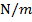 . The work that must be done on the spring to move the object from any starting position x1 to a final position x2 is,
. The work that must be done on the spring to move the object from any starting position x1 to a final position x2 is,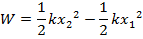
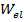 , and is,
, and is,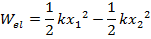
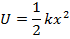
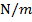 , and the potential energy unit is the Joule (J).
, and the potential energy unit is the Joule (J).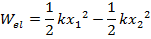
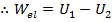
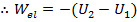
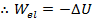
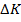 . In this case, the only force that acts on the object is the force of the spring, so the total energy is equal to
. In this case, the only force that acts on the object is the force of the spring, so the total energy is equal to 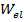 , and
, and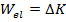
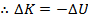
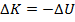
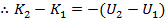
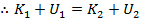
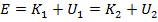
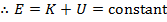 (if the elastic force is the only force doing work)
(if the elastic force is the only force doing work)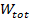 is,
is,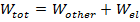
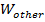 is the work done by all other forces, and
is the work done by all other forces, and 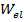 is the work done by the spring. The change in kinetic energy is always equal to the total work,
is the work done by the spring. The change in kinetic energy is always equal to the total work, 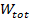 , and so,
, and so,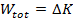
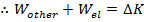
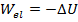 , the equation becomes,
, the equation becomes,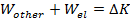
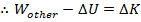
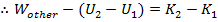
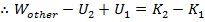
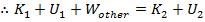 (if the elastic force is not the only force doing work)
(if the elastic force is not the only force doing work)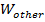 value.
value.
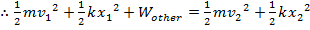 (if forces other than elastic do work)
(if forces other than elastic do work)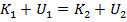 (energy conservation)
(energy conservation) (energy non-conservation)
(energy non-conservation)