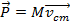Momentum
Momentum is a quantity that can be used to understand things like collisions, without specifically needing to know the forces that act on the objects involved. For example, when a tennis racket hits a ball, the strings of the racket bend, the ball compresses, and numerous other forces affect the outcome. However, by analyzing the momentum of these objects, it is possible to understand a lot about the collision.
Momentum is a vector quantity, and is represented by the symbol
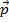
. It is the product of the mass of an object, m, and its velocity vector,
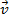
. The definition of momentum is,
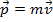
The magnitude of the momentum is,
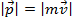
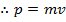
The unit of magnitude of the momentum is the unit of mass times the unit of speed,
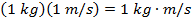
Momentum is expressed in units of
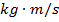
As a vector quantity, momentum can be expressed in terms of components in the principal three axes (x, y, and z). The subscripts for these axes indicate the direction in the formulas,
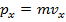
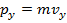
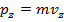 Impulse
Impulse
A quantity that is closely related to momentum is called impulse. Impulse is also a vector quantity, and is represented by the symbol
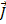
. Impulse is the product of a constant net force,
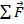
, and a time interval
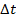
, which is the time interval for which the force is applied. The constant net force is the vector sum of all forces,
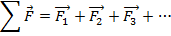
The time interval is the time difference between a starting time t
1 and a later time t
2,
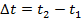
In this formula, the Greek letter

("delta") is used to mean "the change in".
The formula for impulse (assuming a constant net force) is,
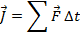
The unit of impulse is the Newton-second,
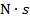
.
By Newton's Second Law, the net force is equal to the mass of an object times its acceleration,
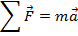
In a previous section, the acceleration was defined to be the change in velocity divided by the change in time,
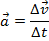
The constant net force is equal to,
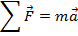
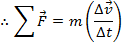
This can be substituted in to the equation for impulse,
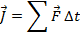
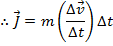
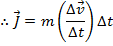
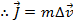
The change in velocity is the difference between the velocities at the starting and ending times,
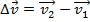
The formula for impulse becomes,
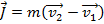
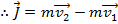
The equation for momentum is
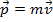
, and so the two terms in the above equation for impulse are momenta at an initial and a final time,
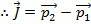
This equation is called the
impulse-momentum theorem. In words, it states that the change in momentum of an object in a certain time interval is equal to the impulse of the net force that acts on the object in the time interval. Using this formula, it is possible to relate changes in momentum to the forces that were applied to cause the change. It also shows that the time over which a force is applied has an effect on the change in momentum that results.
It is also important to note that the units for momentum and impulse are effectively the same. The unit of momentum is
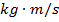
, and the unit of impulse is the Newton-second,
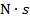
. The Newton is a compound unit, defined as,
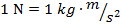
The Newton-second is thus,
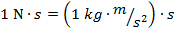
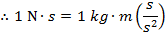
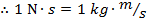 Conservation of Momentum
Conservation of Momentum
When two objects interact, such as in a collision, they may exert forces on each other. The forces the objects exert on each other can be considered part of a
closed or
isolated system. In this case, the forces involved are
internal forces. If any outside forces affect the system, these are called
external forces. According to Newton's Third Law, when there are no external forces, the internal forces that act between two objects have equal magnitudes and opposite directions. If the two objects are labeled
A and
B, the forces they exert on each other are,
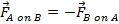
During a collision, these forces act for the same amount of time. If the collision begins at time t
1 and ends at time t
2, then the time duration of the collision is
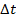
, and the impulse experienced by object A is,
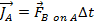
The impulse experienced by object B is,
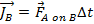
If the values for the forces in these impulse equations are substituted in to the equation for Newton's Third Law, the result is,
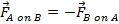
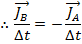
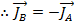
By the impulse-momentum theorem, this is equivalent to,
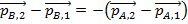
In this equation,
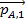
means the momentum of object A at time t
1,
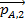
means the momentum of object A at time t
2,
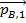
means the momentum of object B at time t
1, and
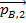
means the momentum of object B at time t
2.
The equation can be rearranged to put all of the terms for time t
1 on one side, and terms for time t
2 on the other,
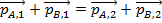
In this case, in which there were no external forces, the sum of the momenta before the collision is equal to the sum of the momenta after. In general, as long as there are no external forces, the total momentum of the system is a constant. This is known as
conservation of momentum.
For any number of objects (labeled A, B, C, etc.), the total momentum can be labeled
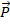
,
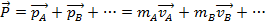
If there are no external forces, the total momentum
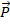
remains constant, even if the momenta of the individual objects change.
Center of Mass Motion
The principle of conservation of momentum is related to the concept of center of mass. If a system contains several objects or particles, labeled A, B, C, etc., in which object A has mass m_A and position vector
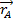
, and so on, then the position vector of the center of mass
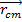
is,
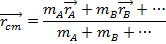
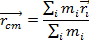
The SI unit of the center of mass position vector is meters, m.
As the objects in the system move, the position vectors change with time. To describe this, the position vectors can be replaced with velocity vectors to obtain a velocity vector for the center of mass
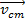
,
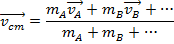
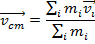
The SI unit of the center of mass velocity vector is meters per second,
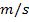
.
The total mass can be defined as,
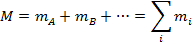
Then, the equation for the velocity vector of the center of mass can be rearranged,
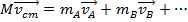
The left side of this equation now has the form of a momentum. So, it can be represented using the label for total momentum of a system
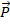
,
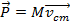
Therefore, the total momentum of a number of objects is equal to the mass times the velocity of the center of mass.
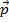 . It is the product of the mass of an object, m, and its velocity vector,
. It is the product of the mass of an object, m, and its velocity vector, 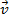 . The definition of momentum is,
. The definition of momentum is,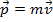
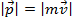
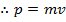
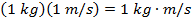
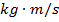
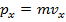
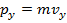
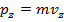
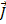 . Impulse is the product of a constant net force,
. Impulse is the product of a constant net force, 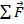 , and a time interval
, and a time interval 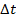 , which is the time interval for which the force is applied. The constant net force is the vector sum of all forces,
, which is the time interval for which the force is applied. The constant net force is the vector sum of all forces,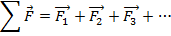
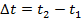
 ("delta") is used to mean "the change in".
("delta") is used to mean "the change in".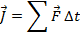
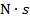 .
.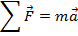
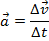
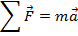
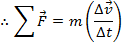
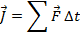
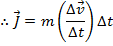
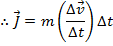
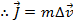
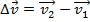
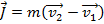
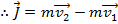
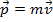 , and so the two terms in the above equation for impulse are momenta at an initial and a final time,
, and so the two terms in the above equation for impulse are momenta at an initial and a final time,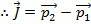
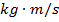 , and the unit of impulse is the Newton-second,
, and the unit of impulse is the Newton-second, 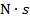 . The Newton is a compound unit, defined as,
. The Newton is a compound unit, defined as,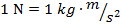
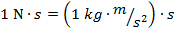
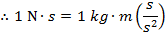
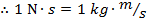
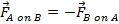
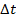 , and the impulse experienced by object A is,
, and the impulse experienced by object A is,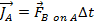
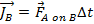
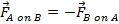
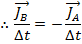
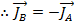
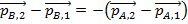
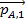 means the momentum of object A at time t1,
means the momentum of object A at time t1, 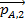 means the momentum of object A at time t2,
means the momentum of object A at time t2, 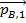 means the momentum of object B at time t1, and
means the momentum of object B at time t1, and 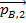 means the momentum of object B at time t2.
means the momentum of object B at time t2.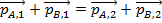
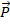 ,
,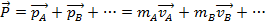
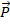 remains constant, even if the momenta of the individual objects change.
remains constant, even if the momenta of the individual objects change.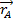 , and so on, then the position vector of the center of mass
, and so on, then the position vector of the center of mass 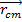 is,
is,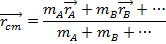
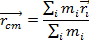
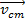 ,
,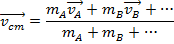
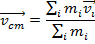
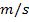 .
.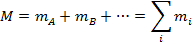
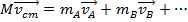
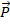 ,
,