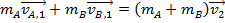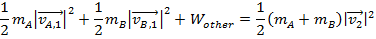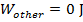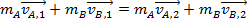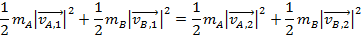Energy and Momentum
Energy and momentum both relate to forces that act on objects, but they are different concepts. The simplest difference between energy and momentum is that energy is a scalar quantity and momentum is a vector. Work and energy (which are equivalent concepts, according to the work-energy theorem) do not have a direction associated with their values (the definition of a scalar). In contrast, momentum has a direction as well as a value (the definition of a vector).
The difference between energy and momentum can be better understood using the related quantity impulse, which was discussed in the previous section. Impulse is equal to a net force,
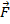
, applied over an interval of time
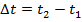
,
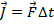
The impulse-momentum theorem states that impulse is also equal to a change in momentum,
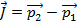
In this formula,
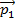
is the momentum at time t
1, and
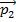
is the momentum at time t
2. The Greek letter

("delta") is used to mean "the change in". Using these formulas, the change in momentum can be written,
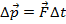
Therefore, a change in momentum is the result of a net force applied for an amount of time.
Work is equivalent to a net force applied over a distance. If this distance is expressed as a difference between two displacements,
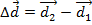
, then the formula for work is,
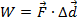
By the work-energy theorem, work is equal to a change in kinetic energy,
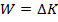
Using these formulas, the change in kinetic energy can be written,
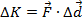
Now, the formulas for the change in momentum and the change in kinetic energy can be compared. The change in momentum is,
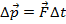
The change in kinetic energy is,
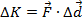
These formulas show that the change in kinetic energy is related to the distance over which a force acts, whereas the change in momentum is related to the time over which a force acts.
An example is the collision between a tennis racket and a tennis ball. The force of contact is the result of the tennis player accelerating the tennis racket toward an incoming ball. When the ball makes contact with the racket, the racket strings bend, the ball compresses, and they briefly travel together. The time they travel together may only be a small fraction of a second, but that brief time is what determines the change in momentum. During this time, the tennis racket travels forward. The distance the racket travels while the ball is in contact determines the change in kinetic energy.
What the above example shows is that momentum and energy are different quantities. What it also shows is that they both change as a result of the same collision. For that reason, they can examined in combination to understand a collision.
Objects involved in a collision exert forces on each other. If these forces are the only ones that act on the objects, then the system can be considered closed or isolated. In this case, the system is said to have only internal forces. In the real world, there are many collisions in which the internal forces are significantly greater than external forces. For example, the air resistance around a bowling ball hitting the pins is a tiny effect compared to the force of the collision. The external forces can be neglected, and the system can be assumed to be closed.
In a system that is closed, or assumed to be closed, momentum is conserved. We will normally assume this to be true for any collisions in AP Physics. However, there are different types of collisions, depending whether or not energy is conserved.
Inelastic Collisions
In an inelastic collision, momentum is conserved, but energy is not. Usually, energy is lost to the system as a result of heating, vibration, deformation of the objects, or other effects. For example, in a collision between two cars, part of the energy of the collision is transferred to bending the metal. Energy is absorbed by the structure of the cars.
If
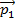
is the total momentum before a collision, and
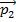
is the momentum after, then for inelastic collisions,
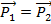
In a previous section, a formula for energy non-conservation was presented,

In this formula, K
1 is the kinetic energy at some initial time, U
1 is the potential energy at the initial time,
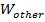
is "other" work, which is either gained or lost to the system, K
2 is the kinetic energy at some later time, and U
2 is the potential energy at the later time. If the times are taken to be immediately before and immediately after a collision, then the position before and after is the same. Potential energy is associated with position, so the potential energy before and after must be the same,
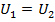
(immediately before and after a collision)
For an inelastic collision, the energy non-conservation formula is therefore,

If energy is lost to the system during the collision,
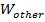
must have a negative value.
These formulas can be re-written for a collision between two objects:
-
Object A with mass mA, pre-collision velocity
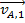 , and post-collision velocity
, and post-collision velocity 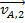
- Object B with mass mB, pre-collision velocity
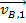 , and post-collision velocity
, and post-collision velocity 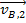
The inelastic collision momentum formula is,
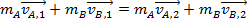
The inelastic collision energy formula is,
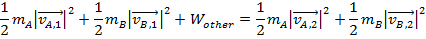 Perfectly Inelastic Collisions
Perfectly Inelastic Collisions
A special case of inelastic collision is called the "perfectly" or "completely" inelastic collision. In a perfectly inelastic collision, two objects collide and stick together. The momentum of the objects before the collision is conserved, but the total energy is not conserved. The final velocity of the combined objects depends on the masses and velocities of the two objects that collided. The objects remain stuck together, so the final velocities must be equal,
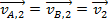
For simplicity, the final velocity of the combined objects can be labeled
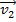
.
The perfectly inelastic collision momentum formula is,
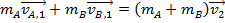
The inelastic collision energy formula is,
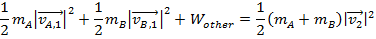 Elastic Collisions
Elastic Collisions
In an elastic collision, both momentum and energy are conserved. In this case, the forces between the colliding objects are conservative. An example of real objects that have (approximately) elastic collisions are billiard balls. These compress at the collision site for an instant, but then spring back. They momentarily store elastic potential energy, but then it is converted back to kinetic energy. No energy is lost during the collision, so there is no work lost to "other" sources,
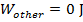
The elastic collision momentum formula is,
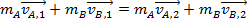
The elastic collision energy formula is,
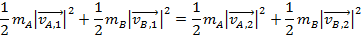 Collisions Summary
Collisions Summary
The momentum and energy conservation rules for collisions can be written in a concise way as follows:
In a collision in which the external forces can be neglected (a closed system), momentum is conserved. This is almost always assumed in AP Physics problems.
In elastic collisions
only, kinetic energy is also conserved. The total kinetic energy before the collision is equal to the total kinetic energy after.
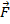 , applied over an interval of time
, applied over an interval of time 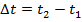 ,
,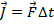
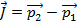
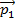 is the momentum at time t1, and
is the momentum at time t1, and 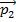 is the momentum at time t2. The Greek letter
is the momentum at time t2. The Greek letter  ("delta") is used to mean "the change in". Using these formulas, the change in momentum can be written,
("delta") is used to mean "the change in". Using these formulas, the change in momentum can be written,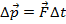
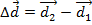 , then the formula for work is,
, then the formula for work is,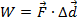
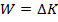
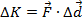
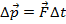
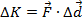
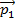 is the total momentum before a collision, and
is the total momentum before a collision, and 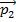 is the momentum after, then for inelastic collisions,
is the momentum after, then for inelastic collisions,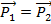

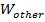 is "other" work, which is either gained or lost to the system, K2 is the kinetic energy at some later time, and U2 is the potential energy at the later time. If the times are taken to be immediately before and immediately after a collision, then the position before and after is the same. Potential energy is associated with position, so the potential energy before and after must be the same,
is "other" work, which is either gained or lost to the system, K2 is the kinetic energy at some later time, and U2 is the potential energy at the later time. If the times are taken to be immediately before and immediately after a collision, then the position before and after is the same. Potential energy is associated with position, so the potential energy before and after must be the same,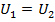 (immediately before and after a collision)
(immediately before and after a collision)
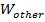 must have a negative value.
must have a negative value.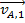 , and post-collision velocity
, and post-collision velocity 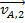
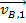 , and post-collision velocity
, and post-collision velocity 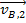
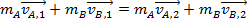
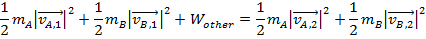
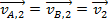
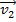 .
.