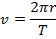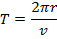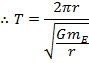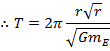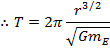Newton's Law of Gravitation
In previous sections, the acceleration due to gravity near the surface of the Earth was used as a constant. The acceleration experienced by all objects was taken to be
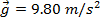
downward. However, this is just an approximation of the conditions near the Earth's surface. In fact, gravity attracts all objects to each other, with a force that depends on the square of the distance between them, and the masses of the objects.
Every object in the universe attracts every other object. The magnitude of the force of gravity between two objects is proportional to the product of their masses, and inversely proportional to the square of the distance. This is Newton's Law of Gravitation, and as a formula it is written,
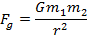
In this formula,
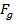
is the magnitude of the force of gravity between two objects, and has units of Newtons (N). The masses of the two objects are labeled m
1 and m
2. In the SI system of units, mass is measured in kilograms (kg). The distance r between the objects is measured in meters (m). The symbol G represents the gravitational constant. The gravitational constant is universal, meaning that it has the same value, no matter which two objects are considered, or where they are located. In SI units, this constant has a value,
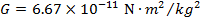
The vector
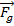
depends on the direction of the force as well as the magnitude. The direction of
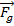
points from the position of object 1 toward object 2. By Newton's Third Law, every force that acts on an object has an opposing force, with an equal magnitude and opposite direction. This is true for objects that experience the force of gravity. If the force that acts from object 1 on object 2 is
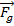
, then the force that acts from object 2 on object 1 is
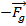
.
When an object experiences the force of gravity from more than one other object, the total force is the vector sum. This is the
superposition of forces, which was mentioned in a previous section.
Weight
The weight of an object is the total gravitational force exerted on the object by every other object in the universe. The weight of an object is labeled w, and its magnitude is equal to the total force of gravity,
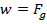
The concept of
weight is different than the concept of
mass. The mass of an object is the same no matter where it is, but weight changes depending on the magnitude of the total force of gravity. The total force of gravity changes depending on the distance from other objects, and so it changes based on the position of an object.
For spherical objects, the distance between the center of mass and the surface is the same at any point. For an object that is much smaller than the sphere, the distance between the centers of mass can be taken to be the radius of the sphere. Planets are approximately spherical, and so for an object sitting on the surface of a planet, the distance used in the force of gravity formula is the planet's radius.
For a small object near the surface of the Earth, the force of gravity of the Earth acting on the object is directed toward the center of the Earth. All other planets, suns, and moons are far away, and so the forces they exert on the object have approximately zero magnitude. The mass of the Earth is labeled m
E, and the radius of the Earth is labeled R
E. Using these values, the magnitude of the force of gravity is,
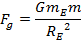
This is also equal to the weight of the object,
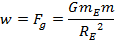
By Newton's Second Law, the weight w is equal to the mass times the acceleration of the object. This can be used to derive the value of gravitational acceleration at the surface of the Earth, g,
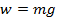
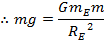
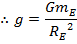
The mass of the Earth is,
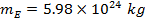
The radius of the Earth is,
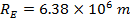
Using these values and the gravitational constant, the value for g at the surface is,
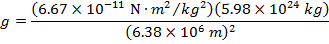
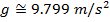 Gravitational Field
Gravitational Field
A general formula for the weight of an object that is some distance from the surface of the Earth is,
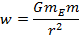
In this formula, r is the distance between the centers of mass. For an object above the surface, the value of r is the sum of the distance above the surface and the radius of the Earth, R
E.
Using Newton's Second Law again, where g(r) is the gravitational acceleration as a function of the distance r,
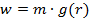
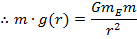
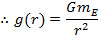
This formula is the distance-dependent value of the acceleration due to gravity. From this formula, the acceleration due to gravity can be found at any position around the Earth. This is known as Earth's
gravitational field. The field extends outward in all directions, with a
field strength that decreases proportional to the square of the distance. The unit of field strength is the same as the unit of acceleration,
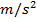
. This unit is equivalent to another that is often used to quote a field strength value, Newtons per kilogram
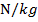
.
Gravitational Potential Energy
In a previous section, potential energy was explained as energy associated with a certain position. Objects with potential energy are able to do work as a result of forces acting on them. A formula for potential energy near the Earth's surface was given as,
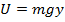
In this formula, y is the distance between the surface of the Earth and the object.
More generally, the potential energy of an object at some distance from the Earth is,
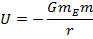
Note that this formula depends on
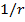
, not on
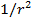
(like the formula for the gravitational force). Also, this potential energy is negative. Since potential energy is associated with position, it is possible for it to have a negative value, depending what position is defined to have a potential energy of zero, U = 0. For this formula, the potential energy approaches zero as the distance r approaches infinity,
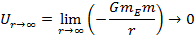
When an object is very far from another, there is almost no potential energy associated with their gravitational attraction.
Motion of Satellites
Satellites orbiting the Earth are constantly in motion, to avoid falling toward the Earth. By maintaining a high velocity, they constantly fall around the Earth, moving in uniform circular motion. In a previous section, the radial (or centripetal) acceleration of objects in circular motion was described. The radial acceleration can be found from the formula,
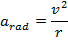
At a distance r from the center of the Earth, the gravitational field strength is,
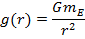
A satellite will maintain a circular path as long as the acceleration due to the gravitational field is the same as the radial acceleration for uniform circular motion. Therefore, an orbiting satellite must have a radial acceleration equal to,
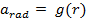
Using this formula, the velocity of a satellite at a distance r can be found.
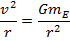
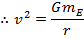
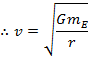
This is the formula for the velocity of a satellite in a
closed or
circular orbit around the Earth. The SI unit of velocity is
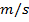
.
The period of the orbit is labeled T. It is the amount of time required for the satellite to complete one full circle around the Earth, and the SI unit of period is seconds. If the radius of the orbit is r, then the circumference of the circle traveled by the satellite is 2πr. The velocity is therefore the distance traveled divided by the period,
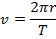
The period is therefore,
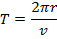
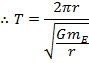
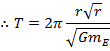
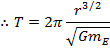
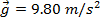 downward. However, this is just an approximation of the conditions near the Earth's surface. In fact, gravity attracts all objects to each other, with a force that depends on the square of the distance between them, and the masses of the objects.
downward. However, this is just an approximation of the conditions near the Earth's surface. In fact, gravity attracts all objects to each other, with a force that depends on the square of the distance between them, and the masses of the objects.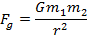
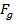 is the magnitude of the force of gravity between two objects, and has units of Newtons (N). The masses of the two objects are labeled m1 and m2. In the SI system of units, mass is measured in kilograms (kg). The distance r between the objects is measured in meters (m). The symbol G represents the gravitational constant. The gravitational constant is universal, meaning that it has the same value, no matter which two objects are considered, or where they are located. In SI units, this constant has a value,
is the magnitude of the force of gravity between two objects, and has units of Newtons (N). The masses of the two objects are labeled m1 and m2. In the SI system of units, mass is measured in kilograms (kg). The distance r between the objects is measured in meters (m). The symbol G represents the gravitational constant. The gravitational constant is universal, meaning that it has the same value, no matter which two objects are considered, or where they are located. In SI units, this constant has a value,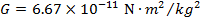
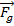 depends on the direction of the force as well as the magnitude. The direction of
depends on the direction of the force as well as the magnitude. The direction of 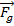 points from the position of object 1 toward object 2. By Newton's Third Law, every force that acts on an object has an opposing force, with an equal magnitude and opposite direction. This is true for objects that experience the force of gravity. If the force that acts from object 1 on object 2 is
points from the position of object 1 toward object 2. By Newton's Third Law, every force that acts on an object has an opposing force, with an equal magnitude and opposite direction. This is true for objects that experience the force of gravity. If the force that acts from object 1 on object 2 is 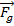 , then the force that acts from object 2 on object 1 is
, then the force that acts from object 2 on object 1 is 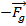 .
.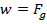
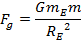
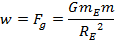
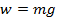
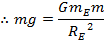
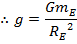
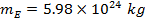
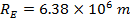
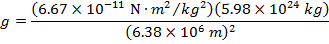
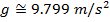
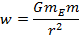
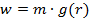
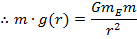
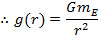
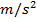 . This unit is equivalent to another that is often used to quote a field strength value, Newtons per kilogram
. This unit is equivalent to another that is often used to quote a field strength value, Newtons per kilogram 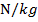 .
.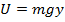
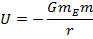
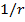 , not on
, not on 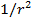 (like the formula for the gravitational force). Also, this potential energy is negative. Since potential energy is associated with position, it is possible for it to have a negative value, depending what position is defined to have a potential energy of zero, U = 0. For this formula, the potential energy approaches zero as the distance r approaches infinity,
(like the formula for the gravitational force). Also, this potential energy is negative. Since potential energy is associated with position, it is possible for it to have a negative value, depending what position is defined to have a potential energy of zero, U = 0. For this formula, the potential energy approaches zero as the distance r approaches infinity,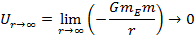
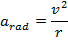
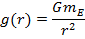
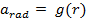
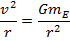
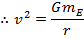
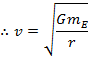
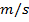 .
.