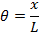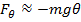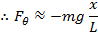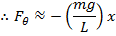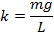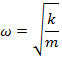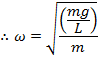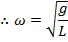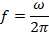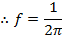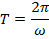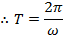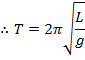Periodic Motion
An object is in periodic motion when its motion repeats with a defined cycle. Periodic motion is also known as oscillation. Common examples are the movement of springs and pendulums, but there are many other situations in which oscillations occur.
The most important features of periodic motion are that the object has a stable equilibrium position, and a restoring force that is directed toward that position. For springs, there is a position at which they are at rest, but when they are either stretched or compressed, there is a restoring force that is always pointed in the direction of the equilibrium position. Pendulums are stable when they hang straight down. If a pendulum is pulled away from this equilibrium position, it swings back and forth as it is acted on by tension force and gravity.
The equilibrium position is defined to be the origin, O. If an object with a certain mass m starts at the origin, and is moved away from it, the distance of its movement is the displacement. For one-dimensional motion in the x-axis, the displacement can be assigned the variable x. The restoring force F
x acts in this axis. The acceleration a
x in the x axis can be found by Newton's second law,
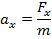
An object that is oscillating in one dimension will move back and forth through the origin. In the ideal (or simple) case, it will move the same distance away from the origin in either direction. This value is called the "amplitude", and is assigned the variable A. The periodic motion of the object will be constrained between x = A and x = -A. Since it is a displacement, the SI unit of A is the meter.
One complete oscillation of an object is called a "cycle". In one cycle, the object can move from displacement A, through the origin to -A, and back to A. The starting point is not important, as long as the object returns to that position. The object moving from O to A, to -A, and back to O is also one cycle.
The time required for the object to move through one cycle is called the "period", T. The SI unit for period is the second, though "seconds per cycle" is often written. It is important to remember that the "cycle" is not a unit, so using it in this way only serves as a placeholder, or a reminder that the time relates to periodic motion.
The inverse of the period is called the "frequency". The frequency f is
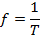
The period is therefore
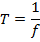
The unit of frequency can be written a number of ways. "Cycles per second" is often written, though remember that "cycle" is not itself a unit. This makes the SI unit of frequency
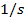
, or
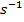
. This unit is also called "Hertz" (Hz), where
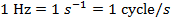
Another useful quantity is the "angular frequency",
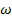
. The angular frequency is equal to 2π times the frequency,
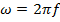
The angular frequency can also be expressed in terms of the period,
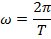
Angular frequency represents the rate of change of an angle. The link between periodic motion and angles is easier to imagine by thinking of the "cycles" of the periodic motion as movement around a circle. The range of angles in one full circle is
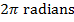
, so
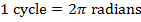
. So, if the unit of the frequency f is
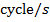
, then the unit of angular frequency is
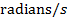
.
Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a special case of periodic motion. In SHM, the restoring force F
x is directly proportional to the displacement x. The restoring force and the displacement always have opposite signs, since the force is always directed back toward the origin. A constant of proportionality k makes it possible to write an equation for the force,
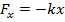
For springs, this relationship is known as Hooke's Law, and k is called the spring constant. The SI unit of k is Newtons per meter,
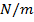
.
The acceleration of an object in simple harmonic motion can be found by combining Newton's second law and Hooke's law,
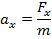
and,
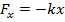
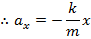
The angular frequency in simple harmonic motion is a constant that only depends on the spring constant and the mass of the object,
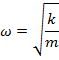
Using this equation and the equations relating the angular frequency to the period and frequency earlier in this section, formulas for the frequency and period in simple harmonic motion can be obtained,
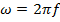
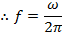
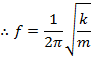
and,
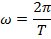
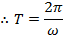
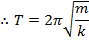
In simple harmonic motion, the displacement of an object can be described using a sinusoidal function in time. These functions (sine or cosine) are ideal for describing periodic or cyclical situations, and simple harmonic motion has a cyclical behavior with respect to time. The general equation for the displacement of an object in simple harmonic motion can be written,
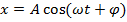
In this equation, A is the amplitude of the motion, which was defined previously in this section. The time, in seconds, is the variable t. There is a "phase angle"
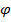
that has units of radians. The phase angle represents a choice of starting position. It is set by the oscillating object's position at the starting time, t = 0. If the starting position is x = A, then the phase angle is
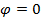
. If the starting position is x = 0 m, then the phase angle is
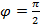 Energy in Simple Harmonic Motion
Energy in Simple Harmonic Motion
For objects in simple harmonic motion, the total mechanical energy is conserved. This means that the energy of the system converts back and forth between kinetic (K) and potential (U) energy, and that the sum of these is always a constant,
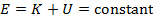
The kinetic energy of the object is related to its velocity,
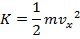
The potential energy of the object in simple harmonic motion is,
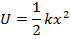
The sum of these is related to the amplitude of the motion,
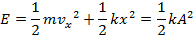 Vertical Springs
Vertical Springs
Imagine one end of a spring is attached to a hook, and the other is attached to an object with mass m and allowed to hang down vertically. In this case, the object will experience two forces. One force will be the restoring force of the spring, directed upward. The other force will be the force of gravity acting on the mass, directed downward. If the mass is not moving, it will hang at rest at an equilibrium position where the net force is zero,
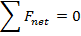
If "up" is defined as the positive x direction, and the position x = 0 is above the equilibrium position, then the sum of forces in the x axis is,
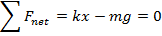
The equilibrium position can be found from the above formula for the sum of forces.
Simple Pendulum
Pendulums are stable when they hang straight down. In this position, the mass at the end of the rod or string is acted on by two forces. These are the tension force in the rod or string, and the force due to gravity. At the equilibrium position, these forces sum to zero. If a pendulum is pulled away from the equilibrium position, it swings back and forth through its equilibrium point. If the angle the rod makes with the vertical axis is θ, then the restoring force is a component of the gravitational force,
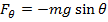
If the angle θ is small, the
small-angle approximation for sinθ can be used to simplify the formula,
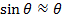
(when the angle θ is small)
If the length of the rod is L, and the displacement in the horizontal axis is x, then,
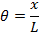
With the small-angle approximation, the restoring force is,
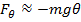
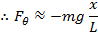
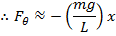
This is now in the form of the spring restoring force for springs, F = -kx. Therefore, the values in front of the x are equal to the spring constant, k,
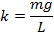
The angular frequency for a simple pendulum is,
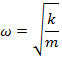
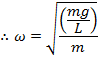
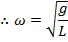
The frequency of the oscillation of a simple pendulum is,
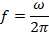
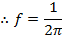
The period of the oscillation of a simple pendulum is,
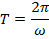
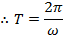
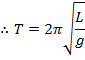
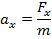
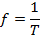
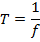
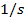 , or
, or 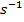 . This unit is also called "Hertz" (Hz), where
. This unit is also called "Hertz" (Hz), where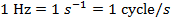
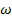 . The angular frequency is equal to 2π times the frequency,
. The angular frequency is equal to 2π times the frequency,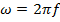
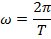
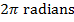 , so
, so 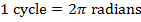 . So, if the unit of the frequency f is
. So, if the unit of the frequency f is 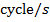 , then the unit of angular frequency is
, then the unit of angular frequency is 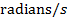 .
.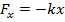
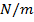 .
.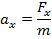
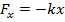
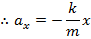
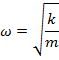
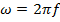
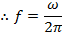
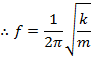
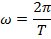
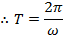
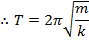
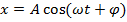
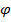 that has units of radians. The phase angle represents a choice of starting position. It is set by the oscillating object's position at the starting time, t = 0. If the starting position is x = A, then the phase angle is
that has units of radians. The phase angle represents a choice of starting position. It is set by the oscillating object's position at the starting time, t = 0. If the starting position is x = A, then the phase angle is 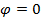 . If the starting position is x = 0 m, then the phase angle is
. If the starting position is x = 0 m, then the phase angle is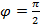
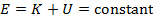
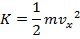
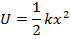
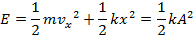
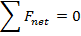
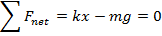
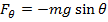
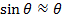 (when the angle θ is small)
(when the angle θ is small)