Kirchhoff's Rules and Resistors in Series and Parallel
Kirchhoff's Rules
Electronic devices contain circuits made up of many elements. Current "flows" through the elements, and when a voltage source is in the circuit, there will be voltage differences across these elements. For a direct-current circuit (meaning that the current does not change with time), the voltage and current at any position in the circuit can be calculated using Kirchhoff's rules.
Within a circuit, there are points we will call "junctions". These are points where three or more conducting lines meet. If we think of current flowing through the circuit in a certain direction, these are places where current splits or combines with current from another line. Junctions are also sometimes called "nodes" or "branch points".
Kirchhoff's junction rule is how current splits and combines at junction points within a circuit with multiple paths. It is a consequence of the conservation of charge. The sum of the currents that flow in to a junction is equal to the sum of the currents that flow out of the junction. Expressed another way, the sum of all currents at a junction must equal zero,
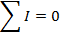
Any complete circuit must contain one or more "loops". Loops are closed conducting paths. Current is not able to flow through a conductor that is not part of a closed loop.
Kirchhoff's loop rule determines how voltage drops along any pathway in a circuit. It is a consequence of the conservation of energy. The sum of the potential differences around any loop must equal zero,
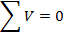
Using these rules, and the formula relating voltage, current, and resistance: V = IR, it is possible to find the current at any point in a circuit, and the potential difference across any component in the circuit. To analyze a circuit, use the two Kirchhoff's rules to create the same number of equations as there are unknown variables. Each sum of voltages around a loop, or sum of currents in and out of a junction is a new equation.
Resistors in Series and Parallel
Combinations of multiple resistors can be simplified by finding an equivalent resistance. The equivalent resistance is the value of a single resistor that can replace the whole combination. The equivalent resistance of a group of resistors can be found using formulas derived using Kirchhoff's rules. These formulas can simplify the analysis of a circuit. The unit of resistance is the Ohm, which is represented with the Greek letter Ω ("omega").
When a number of circuit elements are connected in sequence, with a single current path through all of them, they are connected in series. The total potential difference of a series of resistors is equal to the sum of the voltage drops across each element. If V1, V2, etc. are the voltage drops across the resistors in a series, and V is the total voltage drop,
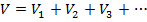
The current through each of these elements is the same, and so using the formula V = IR,
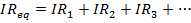
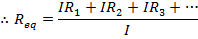
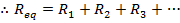
The equivalent resistance of a number of resistors in series is the sum,
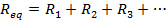
The equivalent resistance of a number of resistors in series is equal to the sum of their individual resistances.
When a number of circuit elements are connected in parallel current paths, so that the voltage across each of them is the same, they are connected in parallel. By Kirchhoff's current rule, at a junction at one end of the parallel paths, the current into the junction must be equal to the current out of the junction. Therefore, the total current splits between the parallel paths. If I is the total current, and I1, I2, etc. are the currents through the individual paths,
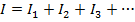
The voltage across each of these elements is the same, and so using the formula V = IR,
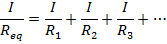
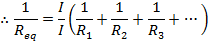
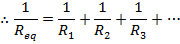
The equivalent resistance of a number of resistors in parallel can be found using the reciprocal of resistance, 1/R. The reciprocal of the equivalent resistance is equal to the sum of the reciprocals of each resistance,
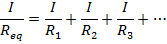
Current and Voltage Measurement
The current or voltage through different parts of a circuit can be measured using an electrical device. The device is known as a d'Arsonval galvanometer, though for simplicity it will just be called a "meter". It consists of a coil of fine wire, mounted on a pivot, placed in a magnetic field, and attached to a spring. When there is an electric current in the coil, the magnetic field exerts a torque on the coil, and it pulls the spring. The restoring torque of the spring is proportional to the current in the coil. If the coil obeys Ohm's law, the current is proportional to the potential difference (voltage) between the terminals of the coil. Depending how the meter is configured and calibrated, it can be used to measure current, voltage, or resistance.
A meter that is configured to measure current is called an ammeter. It measures the current that is passing through it. If it is placed in series in a circuit branch with other circuit components, it can measure the current passing through that branch and components. In circuit diagrams, an ammeter can be represented as a letter "A" inside a circle, in series with other components.
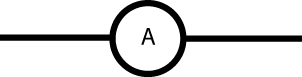
Real ammeters have a small internal resistance, though the lower this internal resistance is, the more accurate the ammeter will be. If a resistor is connected in parallel with the ammeter, the ammeter can be used to measure currents that would otherwise be off scale. This resistor is called a "shunt resistor", and commercial ammeters may have several that the user can switch between to provide a range of measurement scales.
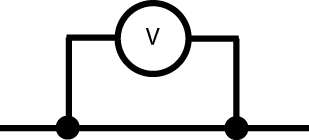
A meter that is configured to measure the voltage is called a voltmeter. A voltmeter measures the potential difference between any two points in a circuit. To do this, it must be connected between those two points, in parallel to any circuit elements between these points. An ideal voltmeter would not allow any of the current in the circuit to flow through it, since that would change the circuit that is being measured. This means that an ideal voltmeter must have infinite resistance. Real voltmeters must have a finite resistance, though the value can be very large to reduce the current that is diverted through the meter. In circuit diagrams, a voltmeter can be represented as a letter "V" inside a circle, in parallel with other components.
Electronic devices contain circuits made up of many elements. Current "flows" through the elements, and when a voltage source is in the circuit, there will be voltage differences across these elements. For a direct-current circuit (meaning that the current does not change with time), the voltage and current at any position in the circuit can be calculated using Kirchhoff's rules.
Within a circuit, there are points we will call "junctions". These are points where three or more conducting lines meet. If we think of current flowing through the circuit in a certain direction, these are places where current splits or combines with current from another line. Junctions are also sometimes called "nodes" or "branch points".
Kirchhoff's junction rule is how current splits and combines at junction points within a circuit with multiple paths. It is a consequence of the conservation of charge. The sum of the currents that flow in to a junction is equal to the sum of the currents that flow out of the junction. Expressed another way, the sum of all currents at a junction must equal zero,
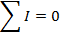
Any complete circuit must contain one or more "loops". Loops are closed conducting paths. Current is not able to flow through a conductor that is not part of a closed loop.
Kirchhoff's loop rule determines how voltage drops along any pathway in a circuit. It is a consequence of the conservation of energy. The sum of the potential differences around any loop must equal zero,
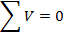
Using these rules, and the formula relating voltage, current, and resistance: V = IR, it is possible to find the current at any point in a circuit, and the potential difference across any component in the circuit. To analyze a circuit, use the two Kirchhoff's rules to create the same number of equations as there are unknown variables. Each sum of voltages around a loop, or sum of currents in and out of a junction is a new equation.
Resistors in Series and Parallel
Combinations of multiple resistors can be simplified by finding an equivalent resistance. The equivalent resistance is the value of a single resistor that can replace the whole combination. The equivalent resistance of a group of resistors can be found using formulas derived using Kirchhoff's rules. These formulas can simplify the analysis of a circuit. The unit of resistance is the Ohm, which is represented with the Greek letter Ω ("omega").
When a number of circuit elements are connected in sequence, with a single current path through all of them, they are connected in series. The total potential difference of a series of resistors is equal to the sum of the voltage drops across each element. If V1, V2, etc. are the voltage drops across the resistors in a series, and V is the total voltage drop,
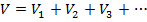
The current through each of these elements is the same, and so using the formula V = IR,
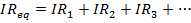
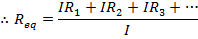
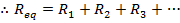
The equivalent resistance of a number of resistors in series is the sum,
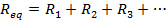
The equivalent resistance of a number of resistors in series is equal to the sum of their individual resistances.
When a number of circuit elements are connected in parallel current paths, so that the voltage across each of them is the same, they are connected in parallel. By Kirchhoff's current rule, at a junction at one end of the parallel paths, the current into the junction must be equal to the current out of the junction. Therefore, the total current splits between the parallel paths. If I is the total current, and I1, I2, etc. are the currents through the individual paths,
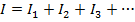
The voltage across each of these elements is the same, and so using the formula V = IR,
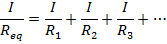
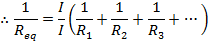
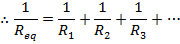
The equivalent resistance of a number of resistors in parallel can be found using the reciprocal of resistance, 1/R. The reciprocal of the equivalent resistance is equal to the sum of the reciprocals of each resistance,
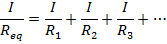
Current and Voltage Measurement
The current or voltage through different parts of a circuit can be measured using an electrical device. The device is known as a d'Arsonval galvanometer, though for simplicity it will just be called a "meter". It consists of a coil of fine wire, mounted on a pivot, placed in a magnetic field, and attached to a spring. When there is an electric current in the coil, the magnetic field exerts a torque on the coil, and it pulls the spring. The restoring torque of the spring is proportional to the current in the coil. If the coil obeys Ohm's law, the current is proportional to the potential difference (voltage) between the terminals of the coil. Depending how the meter is configured and calibrated, it can be used to measure current, voltage, or resistance.
A meter that is configured to measure current is called an ammeter. It measures the current that is passing through it. If it is placed in series in a circuit branch with other circuit components, it can measure the current passing through that branch and components. In circuit diagrams, an ammeter can be represented as a letter "A" inside a circle, in series with other components.

Real ammeters have a small internal resistance, though the lower this internal resistance is, the more accurate the ammeter will be. If a resistor is connected in parallel with the ammeter, the ammeter can be used to measure currents that would otherwise be off scale. This resistor is called a "shunt resistor", and commercial ammeters may have several that the user can switch between to provide a range of measurement scales.
A meter that is configured to measure the voltage is called a voltmeter. A voltmeter measures the potential difference between any two points in a circuit. To do this, it must be connected between those two points, in parallel to any circuit elements between these points. An ideal voltmeter would not allow any of the current in the circuit to flow through it, since that would change the circuit that is being measured. This means that an ideal voltmeter must have infinite resistance. Real voltmeters must have a finite resistance, though the value can be very large to reduce the current that is diverted through the meter. In circuit diagrams, a voltmeter can be represented as a letter "V" inside a circle, in parallel with other components.

|
Related Links: Physics Quizzes AP Physics Notes Vectors and Motion in Two and Three Dimensions |
