Vectors and Motion in Two and Three Dimensions
Vectors in Two and Three Dimensions
A quantity that has only a number and a unit is called a "scalar" value. Mass and temperature are examples. "Vectors" are quantities that have both a magnitude and a direction. Displacement, velocity, and acceleration are all vector quantities. In formulas, to distinguish vectors from scalar values, vectors are written with an arrow above the letter. For example,

The magnitude of a vector is its value without the direction. The symbol for the magnitude of a vector is vertical lines on either side of the letter and arrow, or the letter with the arrow removed,
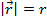
Vectors can also be used in in a two-dimensional plane or a three-dimensional space. A two or three dimensional world can be represented with more than one axis. Each axis is a number line, and is at right angles to the others. In two dimensions, the horizontal axis is labeled the x axis, and the vertical axis is labeled the y axis. In three dimensions, the x axis extends out of the page toward the viewer, the y axis is the horizontal, and the z axis is the vertical.
A vector can be expressed as components, where each component is the portion of the vector in each axis. A vector in two dimensions can be written,
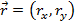
A vector in three dimensions can be written with three components,
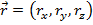
In this vector , rx is the extent of the vector along the x axis, ry is the extent of the vector along the y axis, and rz is the extent of the vector along the z axis. Another way to write this is using unit vectors. Unit vectors have a magnitude of 1, and are identified with a carat ("
, rx is the extent of the vector along the x axis, ry is the extent of the vector along the y axis, and rz is the extent of the vector along the z axis. Another way to write this is using unit vectors. Unit vectors have a magnitude of 1, and are identified with a carat ("  ") over the letter label. A unit vector for
") over the letter label. A unit vector for  can be found by dividing the vector by its magnitude,
can be found by dividing the vector by its magnitude,
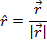
There are special unit vectors that are aligned with the three axes,
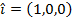
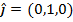
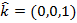
Using these, any vector can be written as a sum of values multiplied by these unit vectors,
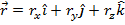
This way of writing the vector shows that vectors can be added. Two vectors
shows that vectors can be added. Two vectors 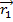 and
and 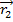 can be added as follows,
can be added as follows,
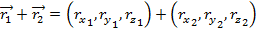
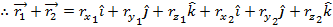
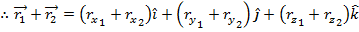
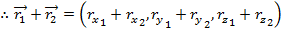
Therefore, vectors can be added by adding their components. The same applies to subtraction. Subtracting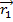 from
from 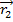 ,
,
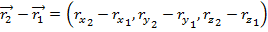
The magnitude of a vector can be found from its components. Since the components are at right angles (perpendicular) to each other, the magnitude can be found using the Pythagorean theorem: the square of the hypotenuse is equal to the sum of the squares of the other sides. The magnitude of the vector can be found by treating it as the hypotenuse of a triangle, and the components are the other sides. For a vector in two dimensions, =(rx,ry ), this means that the magnitude can be found from,
=(rx,ry ), this means that the magnitude can be found from,
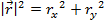
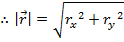
For a vector in three dimensions, = (rx,ry,rz ), the magnitude is,
= (rx,ry,rz ), the magnitude is,
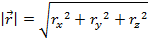
When multiplying numbers, there are three different ways to show that multiplication should be performed: x, ., or no symbol. For example, a multiplied by b can be written a x b, a . b, or ab. Vectors can also be multiplied, but there are different kinds. The three ways to write multiplication have very different meanings for vectors.
A vector can be multiplied by a scalar number c, by writing them with no operator symbol between them,
can be multiplied by a scalar number c, by writing them with no operator symbol between them,
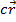
The number increases the magnitude of the vector by the factor c. If the vector is written as components, each component is multiplied by c,
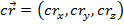
The "dot" or "scalar" product of two vectors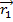 and
and 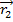 is written
is written 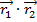 . The result of the dot product is a scalar value, equal to the magnitudes of the vectors multiplied by the cosine of the angle between them θ,
. The result of the dot product is a scalar value, equal to the magnitudes of the vectors multiplied by the cosine of the angle between them θ,
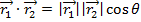
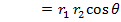
The dot product can also be calculated in terms of the vector components,
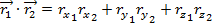
By setting these equal to each other, there is a way to calculate the angle between the vectors,
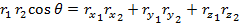
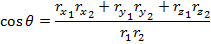
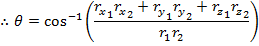
The "cross" or "vector" product of two vectors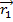 and
and 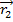 is written
is written 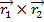 . The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both
. The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both 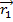 and
and 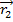 , which is given the label
, which is given the label 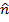 ,
,
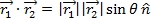
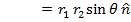
The vector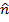 can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).
can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).
Vectors can be broken in to x and y axis components, if the angle between the vector and an axis is known. In two dimensions, the x axis component of has a magnitude rx, and the y axis component has a magnitude of ry. If there is an angle θ between the vector
has a magnitude rx, and the y axis component has a magnitude of ry. If there is an angle θ between the vector  and the x axis, then trigonometry can be used to find the values of rx and ry. The sine of an angle is equal to,
and the x axis, then trigonometry can be used to find the values of rx and ry. The sine of an angle is equal to,
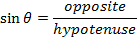
The cosine of an angle is equal to,
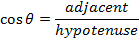
Since θ is the angle between the vector and the x axis, the x component of the vector is the "adjacent" side. The magnitude of the vector is r, which forms the hypotenuse. Therefore,
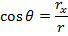
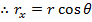
Similarly, the y axis component of the vector is the "opposite" side, and therefore,
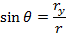
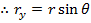
So, in two dimensions the vector can be written,
can be written,
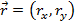
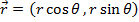
It is also possible to find the magnitude of the vector and the angle from the components rx and ry. The tangent of an angle is,
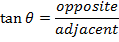
The x component rx is the adjacent side, and the y component ry is the opposite side, and so,
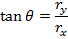
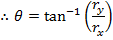
Motion in Two and Three Dimensions
The displacement of an object is a vector, because it has both a distance and a direction. The displacement can be written as a difference between one position vector and another,
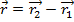
In this form, the magnitude of the displacement is equal to the magnitude of the vector , and the direction of the displacement can be written as a unit vector
, and the direction of the displacement can be written as a unit vector 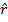 . The position vectors have components, so the vector
. The position vectors have components, so the vector  can be written as,
can be written as,
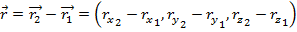
The displacements in the x, y, and z axes can be calculated separately, and added to find the total displacement. Therefore, any kinematic equations meant to calculate displacement in one dimension can be used to find each of the components independently.
Velocity can also be written as a two or three dimensional vector,
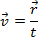
The velocity vector has components,
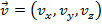
The rate of change of relative to time does not have to be constant. If an object speeds up or slows down, more or less distance is traveled in each unit of time. Between any two times the average velocity is,
relative to time does not have to be constant. If an object speeds up or slows down, more or less distance is traveled in each unit of time. Between any two times the average velocity is,
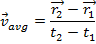
This equation for average velocity can be separated into its components,
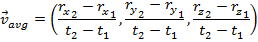
Each component has the same form as the average velocity in one dimension. It is possible to separate the velocity vector and use the formulas for kinematics in one dimension to calculate the velocity component in each axis.
A change in velocity relative to time is called acceleration. Acceleration can be written as a two or three dimensional vector,
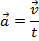
The acceleration vector has components,
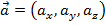
The rate of change of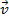 relative to time does not have to be constant. Between any two times the average acceleration is,
relative to time does not have to be constant. Between any two times the average acceleration is,
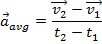
Separating vectors into components can be a very powerful tool when trying to solve physics problems. For example, assume an object has an initial velocity in two dimensions,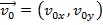 , and an acceleration that only has a component in one axis,
, and an acceleration that only has a component in one axis, 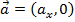 . If you are asked to find the velocity at a later time t, the one-dimensional kinematic formulas can be used to find the velocity in each axis,
. If you are asked to find the velocity at a later time t, the one-dimensional kinematic formulas can be used to find the velocity in each axis,
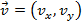
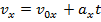
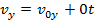
Since the acceleration in the y axis is zero, the velocity in the y direction remains constant,
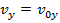
Therefore, the velocity at the later time t is equal to,
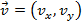
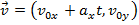
The one-dimensional kinematic formulas can be used to solve two- or three-dimensional motion problems by considering the components separately.
A quantity that has only a number and a unit is called a "scalar" value. Mass and temperature are examples. "Vectors" are quantities that have both a magnitude and a direction. Displacement, velocity, and acceleration are all vector quantities. In formulas, to distinguish vectors from scalar values, vectors are written with an arrow above the letter. For example,

The magnitude of a vector is its value without the direction. The symbol for the magnitude of a vector is vertical lines on either side of the letter and arrow, or the letter with the arrow removed,
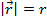
Vectors can also be used in in a two-dimensional plane or a three-dimensional space. A two or three dimensional world can be represented with more than one axis. Each axis is a number line, and is at right angles to the others. In two dimensions, the horizontal axis is labeled the x axis, and the vertical axis is labeled the y axis. In three dimensions, the x axis extends out of the page toward the viewer, the y axis is the horizontal, and the z axis is the vertical.
A vector can be expressed as components, where each component is the portion of the vector in each axis. A vector in two dimensions can be written,
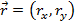
A vector in three dimensions can be written with three components,
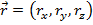
In this vector
 , rx is the extent of the vector along the x axis, ry is the extent of the vector along the y axis, and rz is the extent of the vector along the z axis. Another way to write this is using unit vectors. Unit vectors have a magnitude of 1, and are identified with a carat ("
, rx is the extent of the vector along the x axis, ry is the extent of the vector along the y axis, and rz is the extent of the vector along the z axis. Another way to write this is using unit vectors. Unit vectors have a magnitude of 1, and are identified with a carat ("  ") over the letter label. A unit vector for
") over the letter label. A unit vector for  can be found by dividing the vector by its magnitude,
can be found by dividing the vector by its magnitude,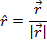
There are special unit vectors that are aligned with the three axes,
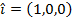
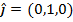
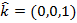
Using these, any vector can be written as a sum of values multiplied by these unit vectors,
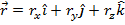
This way of writing the vector
 shows that vectors can be added. Two vectors
shows that vectors can be added. Two vectors 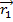 and
and 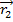 can be added as follows,
can be added as follows,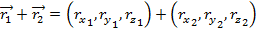
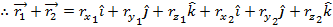
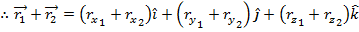
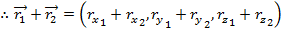
Therefore, vectors can be added by adding their components. The same applies to subtraction. Subtracting
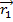 from
from 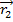 ,
,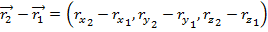
The magnitude of a vector can be found from its components. Since the components are at right angles (perpendicular) to each other, the magnitude can be found using the Pythagorean theorem: the square of the hypotenuse is equal to the sum of the squares of the other sides. The magnitude of the vector can be found by treating it as the hypotenuse of a triangle, and the components are the other sides. For a vector in two dimensions,
 =(rx,ry ), this means that the magnitude can be found from,
=(rx,ry ), this means that the magnitude can be found from,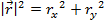
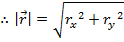
For a vector in three dimensions,
 = (rx,ry,rz ), the magnitude is,
= (rx,ry,rz ), the magnitude is,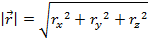
When multiplying numbers, there are three different ways to show that multiplication should be performed: x, ., or no symbol. For example, a multiplied by b can be written a x b, a . b, or ab. Vectors can also be multiplied, but there are different kinds. The three ways to write multiplication have very different meanings for vectors.
A vector
 can be multiplied by a scalar number c, by writing them with no operator symbol between them,
can be multiplied by a scalar number c, by writing them with no operator symbol between them,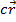
The number increases the magnitude of the vector by the factor c. If the vector is written as components, each component is multiplied by c,
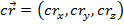
The "dot" or "scalar" product of two vectors
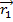 and
and 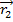 is written
is written 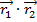 . The result of the dot product is a scalar value, equal to the magnitudes of the vectors multiplied by the cosine of the angle between them θ,
. The result of the dot product is a scalar value, equal to the magnitudes of the vectors multiplied by the cosine of the angle between them θ,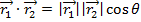
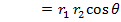
The dot product can also be calculated in terms of the vector components,
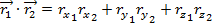
By setting these equal to each other, there is a way to calculate the angle between the vectors,
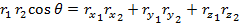
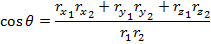
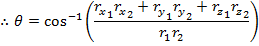
The "cross" or "vector" product of two vectors
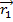 and
and 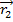 is written
is written 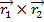 . The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both
. The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both 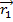 and
and 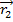 , which is given the label
, which is given the label 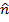 ,
,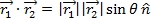
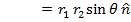
The vector
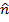 can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).
can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).Vectors can be broken in to x and y axis components, if the angle between the vector and an axis is known. In two dimensions, the x axis component of
 has a magnitude rx, and the y axis component has a magnitude of ry. If there is an angle θ between the vector
has a magnitude rx, and the y axis component has a magnitude of ry. If there is an angle θ between the vector  and the x axis, then trigonometry can be used to find the values of rx and ry. The sine of an angle is equal to,
and the x axis, then trigonometry can be used to find the values of rx and ry. The sine of an angle is equal to,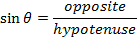
The cosine of an angle is equal to,
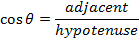
Since θ is the angle between the vector and the x axis, the x component of the vector is the "adjacent" side. The magnitude of the vector is r, which forms the hypotenuse. Therefore,
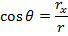
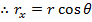
Similarly, the y axis component of the vector is the "opposite" side, and therefore,
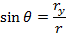
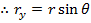
So, in two dimensions the vector
 can be written,
can be written,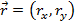
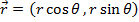
It is also possible to find the magnitude of the vector and the angle from the components rx and ry. The tangent of an angle is,
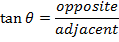
The x component rx is the adjacent side, and the y component ry is the opposite side, and so,
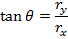
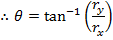
Motion in Two and Three Dimensions
The displacement of an object is a vector, because it has both a distance and a direction. The displacement can be written as a difference between one position vector and another,
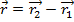
In this form, the magnitude of the displacement is equal to the magnitude of the vector
 , and the direction of the displacement can be written as a unit vector
, and the direction of the displacement can be written as a unit vector 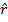 . The position vectors have components, so the vector
. The position vectors have components, so the vector  can be written as,
can be written as,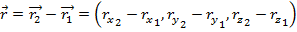
The displacements in the x, y, and z axes can be calculated separately, and added to find the total displacement. Therefore, any kinematic equations meant to calculate displacement in one dimension can be used to find each of the components independently.
Velocity can also be written as a two or three dimensional vector,
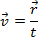
The velocity vector has components,
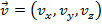
The rate of change of
 relative to time does not have to be constant. If an object speeds up or slows down, more or less distance is traveled in each unit of time. Between any two times the average velocity is,
relative to time does not have to be constant. If an object speeds up or slows down, more or less distance is traveled in each unit of time. Between any two times the average velocity is,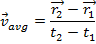
This equation for average velocity can be separated into its components,
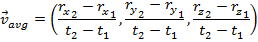
Each component has the same form as the average velocity in one dimension. It is possible to separate the velocity vector and use the formulas for kinematics in one dimension to calculate the velocity component in each axis.
A change in velocity relative to time is called acceleration. Acceleration can be written as a two or three dimensional vector,
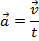
The acceleration vector has components,
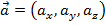
The rate of change of
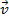 relative to time does not have to be constant. Between any two times the average acceleration is,
relative to time does not have to be constant. Between any two times the average acceleration is,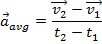
Separating vectors into components can be a very powerful tool when trying to solve physics problems. For example, assume an object has an initial velocity in two dimensions,
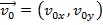 , and an acceleration that only has a component in one axis,
, and an acceleration that only has a component in one axis, 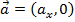 . If you are asked to find the velocity at a later time t, the one-dimensional kinematic formulas can be used to find the velocity in each axis,
. If you are asked to find the velocity at a later time t, the one-dimensional kinematic formulas can be used to find the velocity in each axis,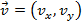
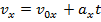
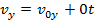
Since the acceleration in the y axis is zero, the velocity in the y direction remains constant,
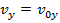
Therefore, the velocity at the later time t is equal to,
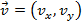
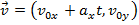
The one-dimensional kinematic formulas can be used to solve two- or three-dimensional motion problems by considering the components separately.
|
Related Links: Physics Quizzes AP Physics Notes Projectile Motion |
