Projectile Motion
A projectile is an object that is given an initial velocity, and then acted on by gravity. The path that the object follows is determined by these effects. This path is called the object's trajectory. The trajectory of a projectile depends on motion in two dimensions. The x component is the horizontal motion of the projectile, and the y component is the vertical motion of the projectile. The units to express the horizontal and vertical distances are meters (m). The horizontal and vertical velocities are expressed in meters per second (m/s).
Given an initial set of conditions, it is possible to calculate the position or velocity of an object at any time t. The displacement of the projectile at any time is represented by the vector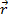 , which has a horizontal component x and a vertical component y,
, which has a horizontal component x and a vertical component y,
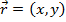
The velocity of the projectile at any time is represented by the velocity vector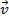 . The vector has a horizontal velocity component vx, and a vertical velocity component vy,
. The vector has a horizontal velocity component vx, and a vertical velocity component vy,
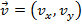
Likewise, the initial velocity vector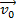 has both x and y components,
has both x and y components,
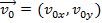
Projectiles do not have an initial acceleration, once they are separated from whatever object launched them (for example, a person's hand throwing the object, or a cannon firing it). Once a projectile is in motion, it is in freefall. The only acceleration acting on it is the downward acceleration due to gravity. The acceleration due to gravity (on Earth) has a magnitude of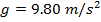 .
.
Projectile Motion Formulas
The one-dimensional kinematic formulas can be used to derive formulas specific to projectile motion. The position of the projectile at time t can be found from the formulas,
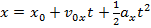
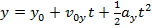
We choose the initial position of the projectile to be,
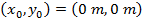
The only acceleration is due to gravity, and so there is no horizontal acceleration,
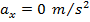
The horizontal distance is,
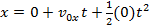
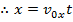
Since we define the positive y direction to be upward, the acceleration in the vertical axis is -g. The vertical distance is,
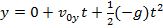
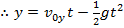
The velocity of the projectile at time t can be found from the formulas,
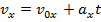
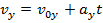
Again, the only acceleration is due to gravity, and so there is no horizontal acceleration. The horizontal velocity is,
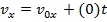
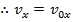
The velocity in the vertical axis is,
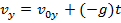
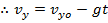
Summary
The formulas for projectile motion are,
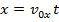
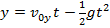
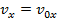
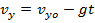
Separating Vector Components
In many physics exercises, the vector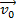 is not given with separate horizontal and vertical components. If the vector magnitude v0 and the angle θ between it and the horizontal axis are known, the initial velocity components are,
is not given with separate horizontal and vertical components. If the vector magnitude v0 and the angle θ between it and the horizontal axis are known, the initial velocity components are,
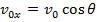
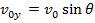
These can then be used in the projectile motion equations.
Combining Vector Components
Many physics exercises ask for the calculated magnitude of the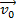 ,
, 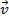 , or
, or 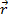 vectors, and their angles relative to the horizontal axis. The components of the initial velocity given above can be used to calculate the magnitude of
vectors, and their angles relative to the horizontal axis. The components of the initial velocity given above can be used to calculate the magnitude of 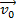 by adding their squares,
by adding their squares,
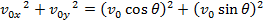
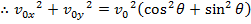
The formula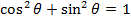 , so
, so
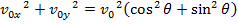
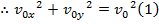
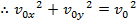
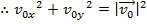
Therefore, the magnitude of the vector can be found using the sum of squares of the components,
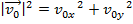
The overall velocity of an object can be found with vector addition of the x and y components: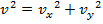 .
.
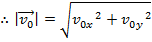
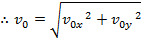
The angle between the vector and the horizontal axis can be found by dividing the y axis component by the x axis component,
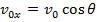
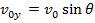
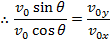
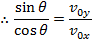
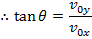
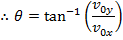
The magnitude of the final velocity v can be found using the sum of squares of the components,
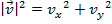
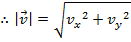
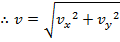
The magnitude of the displacement r can be found from the displacement components,
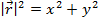
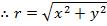
Given an initial set of conditions, it is possible to calculate the position or velocity of an object at any time t. The displacement of the projectile at any time is represented by the vector
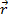 , which has a horizontal component x and a vertical component y,
, which has a horizontal component x and a vertical component y,
The velocity of the projectile at any time is represented by the velocity vector
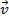 . The vector has a horizontal velocity component vx, and a vertical velocity component vy,
. The vector has a horizontal velocity component vx, and a vertical velocity component vy,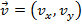
Likewise, the initial velocity vector
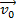 has both x and y components,
has both x and y components,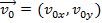
Projectiles do not have an initial acceleration, once they are separated from whatever object launched them (for example, a person's hand throwing the object, or a cannon firing it). Once a projectile is in motion, it is in freefall. The only acceleration acting on it is the downward acceleration due to gravity. The acceleration due to gravity (on Earth) has a magnitude of
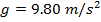 .
.Projectile Motion Formulas
The one-dimensional kinematic formulas can be used to derive formulas specific to projectile motion. The position of the projectile at time t can be found from the formulas,
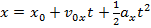
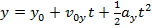
We choose the initial position of the projectile to be,
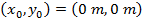
The only acceleration is due to gravity, and so there is no horizontal acceleration,
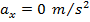
The horizontal distance is,
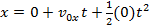
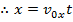
Since we define the positive y direction to be upward, the acceleration in the vertical axis is -g. The vertical distance is,
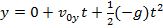
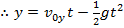
The velocity of the projectile at time t can be found from the formulas,
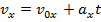
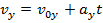
Again, the only acceleration is due to gravity, and so there is no horizontal acceleration. The horizontal velocity is,
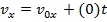
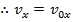
The velocity in the vertical axis is,
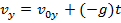
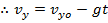
Summary
The formulas for projectile motion are,
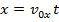
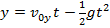
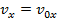
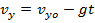
Separating Vector Components
In many physics exercises, the vector
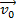 is not given with separate horizontal and vertical components. If the vector magnitude v0 and the angle θ between it and the horizontal axis are known, the initial velocity components are,
is not given with separate horizontal and vertical components. If the vector magnitude v0 and the angle θ between it and the horizontal axis are known, the initial velocity components are,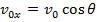
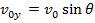
These can then be used in the projectile motion equations.
Combining Vector Components
Many physics exercises ask for the calculated magnitude of the
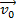 ,
, 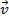 , or
, or 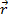 vectors, and their angles relative to the horizontal axis. The components of the initial velocity given above can be used to calculate the magnitude of
vectors, and their angles relative to the horizontal axis. The components of the initial velocity given above can be used to calculate the magnitude of 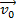 by adding their squares,
by adding their squares,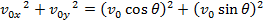
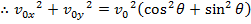
The formula
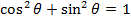 , so
, so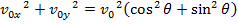
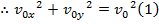
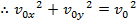
Therefore, the magnitude of the vector can be found using the sum of squares of the components,
The overall velocity of an object can be found with vector addition of the x and y components:
 .
.
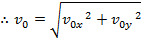
The angle between the vector and the horizontal axis can be found by dividing the y axis component by the x axis component,
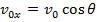
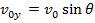
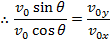
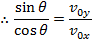
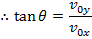
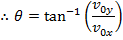
The magnitude of the final velocity v can be found using the sum of squares of the components,
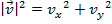
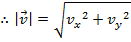
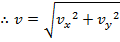
The magnitude of the displacement r can be found from the displacement components,
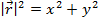
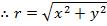
|
Related Links: Physics Quizzes AP Physics Notes Kirchhoff's Rules and Resistors in Series and Parallel |
