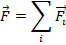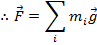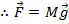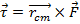Equilibrium Conditions
An object is in equilibrium when it is stationary, even though it is acted on by a number of forces. This requires that the effects of these forces are balanced. This not only applies to forces that act on the center of mass of the object, it also requires that the torques on the object are balanced.
For an extended object like a ladder, forces can act at multiple points. The force of gravity acts on the ladder's center of mass, if the ladder is leaning against a wall there are forces of friction acting on the two ends, and a person climbing the ladder exerts an additional force. If the forces and torques that act on the ladder are not in equilibrium, the ladder may slide or fall.
The
first condition for equilibrium is that the net external force is equal to zero. Expressed in vector form, the first condition is stated,
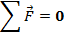
For this vector equation to be true, the sum of the magnitudes of the forces in each axis must be zero,
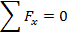
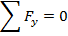
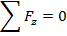
The
second condition for equilibrium is that the object must have no tendency to rotate. This means that the sum of the torques must be zero, for any given axis on the object. Expressed in vector form, the second condition is stated,
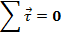
These two conditions for equilibrium result in a system that has no tendency to accelerate linearly, or angularly. It is in equilibrium both translationally and rotationally. Another set of conditions must be met for an object to be in
static equilibrium. Static equilibrium requires an object to be at rest, both translationally and rotationally. An object in static equilibrium must have no linear or angular velocity. Expressed in vector form, static equilibrium requires,
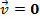
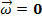
In these formulas,
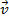
is the linear velocity of the object, and
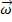
is the angular velocity of the object.
For example, an airplane that is maintaining a fixed altitude and velocity has balanced forces acting on it, meaning that it is in equilibrium. However, because it is maintaining a constant velocity, it is
not in static equilibrium.
Center of Gravity
For the forces on an object to be in equilibrium, the force of gravity on the object must be accounted for. In the discussion of torque, the effect of the distance between a force and a rotation axis was described. For a long object with mass, gravity acts on every point, and so no matter what rotation axis is assumed, the force of gravity exerts a torque on the rest of the object. However, it is possible to find a single point on the object that can be treated as the position at which the force of gravity acts. This position is called the
center of gravity.
In a previous section, the concept of the center of mass was introduced. It is possible to show that, as long as the force of gravity on every part of an object is the same (usually a good assumption), the center of mass and center of gravity will be at the same position.
If we imagine the object broken in to many particles, and each of these is assigned a number, we can sum the effect of gravity on each of these particles. Every particle is assigned a number, and the letter i represents that number. So, the ith particle has mass m
i, and vector position
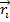
. The vector position can also be expressed as coordinates,
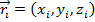
This means that the center of mass can also be expressed as both a vector and as coordinates,
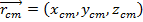
In this formula, the subscript "cm" is used to label the center of mass.
Each coordinate in the vector for the center of mass can be written separately as,
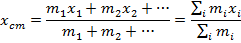
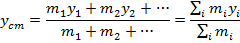
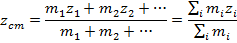
Expressed as a vector, the center of mass is,
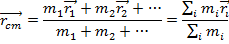
The torque on each particle can be written in terms of the position of the particle and the force of gravity acting on it.
The force of gravity acting on the ith particle can be written,
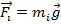
In this formula, the acceleration due to gravity is labeled
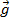
, and it is assumed to be the same for all of the particles. Using this formula for the force, the torque on the
ith particle is,
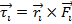
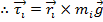
The total torque, as a result of the gravitational force on all of the particles in the object is,
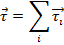
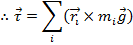
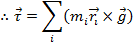
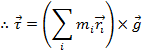
The total mass can be labeled M, and defined as the sum of the particle masses,
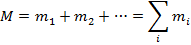
The formula for the total torque can be multiplied and divided by M,
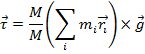
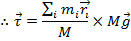
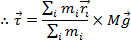
The left side of the cross product in this formula is equal to the center of mass
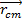
. The right side of the cross product is the total force of gravity
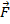
acting on the object,
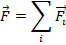
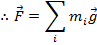
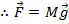
The total torque acting on the object can therefore be written,
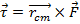
This means that the total torque acting on the object is equal to the cross product of its center of mass position and the total force of gravity on the object.
In summary, to find the torque as a result of gravity acting on an object, find the vector between the axis and the center of mass of the object, and calculate the cross product of that vector and the force of gravity on the object.
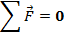
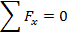
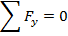
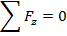
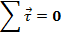
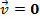
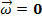
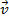 is the linear velocity of the object, and
is the linear velocity of the object, and 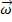 is the angular velocity of the object.
is the angular velocity of the object.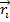 . The vector position can also be expressed as coordinates,
. The vector position can also be expressed as coordinates,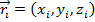
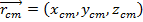
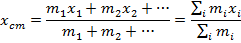
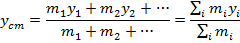
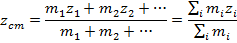
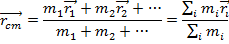
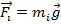
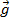 , and it is assumed to be the same for all of the particles. Using this formula for the force, the torque on the ith particle is,
, and it is assumed to be the same for all of the particles. Using this formula for the force, the torque on the ith particle is,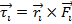
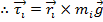
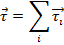
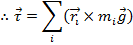
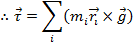
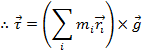
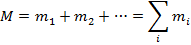
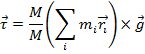
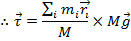
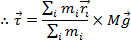
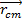 . The right side of the cross product is the total force of gravity
. The right side of the cross product is the total force of gravity 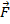 acting on the object,
acting on the object,