Ellipse: Eccentricity

A circle can be described as an ellipse that has a distance from the center to the foci equal to 0. The greater the distance between the center and the foci determine the ovalness of the ellipse. Thus the term eccentricity is used to refer to the ovalness of an ellipse.

If an ellipse is close to circular it has an eccentricity close to zero. If an ellipse has an eccentricity close to one it has a high degree of ovalness.

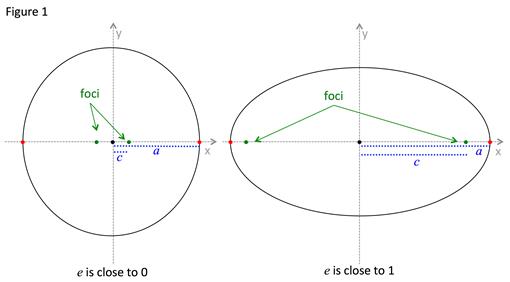
Figure 1 shows a picture of two ellipses one of which is nearly circular with an eccentricity close to zero and the other with a higher degree of eccentricity.

The formal definition of eccentricity is:

ECCENTRICITY OF AN ELLIPSE:

The eccentricity (e) of an ellipse is the ratio of the distance from the center to the foci (c) and the distance from the center to the vertices (a).

$e = \frac{c}{a}$

As the distance between the center and the foci (c) approaches zero, the ratio of

\frac{c}{a}

approaches zero and the shape approaches a circle. A circle has eccentricity equal to zero.

As the distance between the center and the foci (c) approaches the distance between the center and the vertices (a), the ratio of

\frac{c}{a}

approaches one. An ellipse with a high degree of ovalness has an eccentricity approaching one.

Let's use this concept in some examples:

Example 1: Find the eccentricity of the ellipse

\frac{x^{2}}{9} + \frac{y^{2}}{16} = 1

Step 1: Determine the values for the distance between the center and the foci (c) and the distance between the center and the vertices (a).

Length of a: The given equation for the ellipse is written in standard form. Since the major axis is 2a and the smaller minor axis is 2b, then a² > b², therefore a² = 16.

$a^{2} = 16 \to a = 4$

Length of c: To find c the equation c² = a² + b² can be used but the value of b must be determined. From our discussion above, b² = 9. Find b and solve for c.

$b^{2} = 9 \to b = 3$

$c^{2} = 4^{2} - 3^{2} \to c^{2} = 7 \to c = \sqrt{7}$

Step 2: Substitute the values for c and a into the equation for eccentricity.

$e = \frac{c}{a}$

$e = \frac{\sqrt{7}}{4} \to e \approx 0.66$

Example 2: Find the standard equation of the ellipse with vertices at (4, 2) and (-6, 2) with an eccentricity of

\frac{4}{5}

Step 1: Determine the following:

➢ the orientation of the major axis.

➢ the coordinates of the center (h, k).

➢ the length of half the major axis (a).

➢ the distance of half the minor axis (b).

Orientation of major axis: Since the two vertices fall on the horizontal line y = 2, the major axis is horizontal.

Center: Since the vertices are equidistant from the center of the ellipse the center can be determine by finding the midpoint of the vertices.

$(h, k) = (\frac{4 + (- 6)}{2}, \frac{2 + 2}{2}) = (- \frac{2}{2}, \frac{4}{2}) = (- 1, 2)$

Length of a: the length of a is the distance between the center and the vertices. To find a take one of the vertices and determine the distance from the center.

Vertex (4, 2): $c = | 4 - (- 1) | = | 5 | = 5$

Vertex (-6, 2): $c = | - 6 - (- 1) | = | - 5 | = 5$

a = 5

Length of b: To find b the equation c² = a² - b²can be used but the value of c must be determined. Since the eccentricity is $\frac{4}{5}$ the length of c can be found using the value for a. Then solve for b.

$e = \frac{4}{5} = \frac{c}{a}$

$\frac{4}{5} = \frac{c}{5} \to 20 = 5 c \to c = 4$

$c^{2} = a^{2} - b^{2} \to b = \sqrt{a^{2} - c^{2}}$

$b = \sqrt{5^{2} - 4^{2}} \to b = \sqrt{9} \to b = 3$

Step 2: Substitute the values for h, k, a and b into the equation for an ellipse with a horizontal major axis.

Horizontal major axis equation:

$\frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}}$

Substitute values:

$\frac{{[x - (- 1)]}^{2}}{5^{2}} + \frac{{(y - 2)}^{2}}{3^{2}} = 1$

Simplify:

$\frac{{(x + 1)}^{2}}{5^{2}} + \frac{{(y - 1)}^{2}}{3^{2}} = 1$

Related Links:
Math
algebra
Hyperbola: Standard Equation
Hyperbola: Asymptotes
Pre Calculus

To link to this Ellipse: Eccentricity page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/ellipse_eccentricity/">Ellipse: Eccentricity</a>

Ellipse: Eccentricity

More Topics

Educational Videos