Hyperbola: Standard Equation
DEFINITION OF A HYPERBOLA:
The set of all points (x, y) in a plane the difference of whose distances from two fixed points, called foci, is a positive constant.
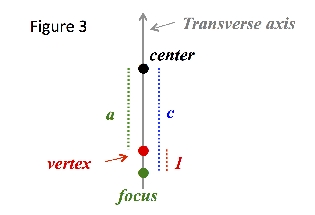
Figure 1 shows a picture of a hyperbola with a vertical transverse axis:
Thus for all (x, y), d2 - d1 = constant. When talking about a hyperbola, the following terms are used:
- The foci are two fixed points equidistant from the center on opposite sides of the transverse axis.
- The vertices are the points on the hyperbola that fall on the line containing the foci.
- The line segment connecting the vertices is the transverse axis.
- The midpoint of the transverse axis is the center.
- The hyperbola has two disconnected curves called branches.
Figure 1 shows a hyperbola with a vertical transverse axis. However a hyperbola could also have a transverse axis that is horizontal as shown in Figure 2.
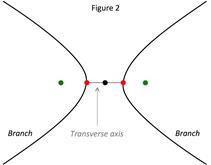
The standard equation of a hyperbola is:
STANDARD EQUATION OF A HYPERBOLA:
➢ Center coordinates (h, k)
➢ a = distance from vertices to the center
➢ c = distance from foci to center
➢
transverse axis is horizontal
transverse axis is vertical
Let's use these equations in some examples:
|
Step 1: Determine the following:
➢ the orientation of the transverse axis.
➢ the coordinates of the center (h , k).
➢ the distance from the vertices to the center (a).
➢ the distance of (b).
|
Orientation of major axis: Since the two foci and two vertices fall on the horizontal line y = 8, the transverse axis is horizontal. Center: The transverse axis is the line segment that connects the two vertices. Since the center is the midpoint of the transverse axis then it is also the midpoint of the two vertices.
Length of a: Take one of the vertices and determine the length to the center. Foci (-1, 8): Foci (5, 8): a = 3 Length of b: To find b the equation can be used but the value of c must be determined. Since c is the distance from the foci to the center, take either foci and determine the distance to the center. Then solve for b. Foci (-3, 8): Foci (7, 8): c = 5
b = 4 |
|
Step 2: Substitute the values for h, k, a and b into the equation for a hyperbola with a transverse axis. |
Equation for a horizontal transverse axis:
Substitute:
|
|
Step 1: Determine the following:
➢ the orientation of the transverse axis.
➢ the coordinates of the center (h, k).
➢ the distance from the vertices to the center (a).
➢ The distance of (b).
|
Orientation of major axis: Since the two foci fall on the vertical line x = 3, the transverse axis is vertical. Center: The center is the midpoint of the two foci.
Length of a: The value of a is the distance between the center and the vertices. Since given the distance from the vertices to the foci of one the value of a can be determined by finding the distance from the foci to the center and subtracting one. To find c take either foci and calculate the distance to the center. Then solve for a. Foci (3, -5): Foci (3, 5): c = 5
Length of b: To find b the equation can be used.
b = 3 |
|
Step 2: Substitute the values for h, k, a and b into the equation for a hyperbola with a vertical transverse axis. |
Equation for a vertical transverse axis:
Substitute:
|
|
Related Links: Math algebra Hyperbola: Asymptotes Polar Coordinates: Coordinate Conversion Pre Calculus |
To link to this Hyperbola: Standard Equation page, copy the following code to your site: