Home > Math > Pre Calculus > Inverse Functions: Finding Inverse Functions Analytically

Inverse Functions: Finding Inverse Functions Analytically

Finding an inverse function for f(x) = x - 1 is easily done by inspection, f -1(x) = x + 1. However for more complicated functions follow these guidelines.

DEFINITION OF ONE-TO-ONE:


  • Graph the function and apply the Horizontal Line Test to determine if the function is one-to-one and thus has an inverse function.

  • Take the function equation and replace f(x) by y.

  • Switch the x and the y in the function equation and solve for y.

  • Replace y by f -1(x).

  • Verify that f(x) and f -1(x) are inverse functions.

º Show that f[f -1(x)] = x.
º Show that f[f -1(x)] = x.
º Show that the domain and range have been reversed.

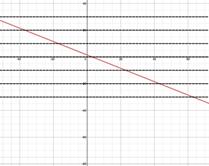
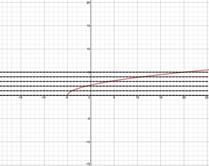
Here is a review of the Horizontal Line Test.

HORIZONTAL LINE TEST:


A function f is one-to-one and has an inverse function if and only if no horizontal line intersects the graph of f at more than one point.



Let's use these guidelines to determine the inverse of a function.

Example 1: Find the inverse function for f( x )= 3−x 2 .

Step 1: Graph the function and apply the Horizontal Line Test to determine if the function is one-to-one and thus has an inverse function.


No horizontal line intersects the graph in more than one place. Thus the function is one-to-one and has an inverse function.

Step 2: Take the function equation and replace f(x) by y.

f( x )= 3−x 2


y= 3−x 2

Step 3: Switch the x and y in the function equation and solve for y.

y= 3−x 2 Original


x= 3−y 2  Switch x and y


2x = 3 - y   Multiply by 2


y + 2x = 3  Add y


y = 3 - 2x   Subtract 2x

Step 4: Replace y by f -1(x).

y = 3 - 2x


f -1(x) = 3 - 2x

Step 5: Verify that f(x) and f -1(x) are inverse functions.


1. Show that f[f -1(x)] = x.


2. Show that f -1[f(x)] = x.


3. Show that the domain and range have been reversed.


1. f[ f −1 ( x ) ]=f( 3−2x )= 3−( 3−2x ) 2 = 3−3+2x 2 = 2x 2 =x


2. f −1 [ f( x ) ]= f −1 ( 3−x 2 )=3−2( 3−x 2 )=3−( 3−x )=3−3+x=x


3.

x

f( x )= 3−x 2

x

f −1 ( x )=3−2x

0

1.5

1.5

0

1

1

1

1

2

0.5

0.5

2

3

0

0

3


Verified, the inverse function of f( x )= 3−x 2 is f −1 ( x )=3−2x

Example 2: Find the inverse function for f( x )= x+5 .

Step 1: Graph the function and apply the Horizontal Line Test to determine if the function is one-to-one and thus has an inverse function.


No horizontal line intersects the graph in more than one place. Thus the function is one-to-one and has an inverse function.

Step 2: Take the function equation and replace f(x) by y.

f( x )= x+5


y= x+5

Step 3: Switch the x and y in the function equation and solve for y.

y= x+5 Original


x= y+5 Switch x and y


x 2 =y+5   Square


x 2 −5=y   Subtract 5

Step 4: Replace y by f -1(x).

y= x 2 −5


f −1 ( x )= x 2 −5

Step 5: Verify that f(x) and f -1(x) are inverse functions.


4. Show that f[f -1(x)] = x.


5. Show that f -1[f(x)] = x.


6. Show that the domain and range have been reversed.


1. f[ f −1 ( x ) ]=f( x 2 −5 )= ( x 2 −5 )+5 = x 2 =x


2. f −1 [ f( x ) ]= f −1 ( x+5 )= ( x+5 ) 2 −5=( x+5 )−5=x


3.

x

f( x )= x+5

x

f −1 ( x )= x 2 −5

0

5

5

0

1

6

6

1

2

7

7

2

3

8

8

3


Verified, the inverse function of f( x )= x+5 is f −1 ( x )= x 2 −5





Related Links:
Math
algebra
Conics: Classifying from General Equation
Component Form and Magnitude
Pre Calculus


To link to this Inverse Functions: Finding Inverse Functions Analytically page, copy the following code to your site: